题目内容
16.△ABC中,点A(1,2),B(-1,3),C(3,-3).(1)求AC边上的高所在直线的方程;
(2)求AB边上的中线的长度.
分析 (1)由斜率公式易知kAC,由垂直关系可得AC边上的高所在的直线方程的斜率k,代入点斜式易得;
(2)求得线段AB的中点坐标为M(0,$\frac{5}{2}$),然后利用两点间的距离公式进行解答.
解答 解:(1)由斜率公式易知kAC=-$\frac{-3-2}{3-1}$=-$\frac{5}{2}$,
∴AC边上的高所在的直线的斜率k=$\frac{2}{5}$,
又AC边上的高所在的直线过点B(-1,3),代入点斜式易得y-3=$\frac{2}{5}$(x+1),
整理,得:2x-5y+17=0.
(2)由A(1,2),B(-1,3)得到AB边的中点坐标M是(0,$\frac{5}{2}$),
故中线长|CM|=$\sqrt{{3}^{2}+(\frac{11}{2})^{2}}$=$\frac{\sqrt{157}}{2}$.
点评 本题主要考查直线方程的求法以及斜率公式,求出相应直线的斜率是解题的关键.

练习册系列答案
相关题目
6.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足1+cosA=$\frac{{\sqrt{3}}}{3}$sinA,sin(B+C)=6cosBsinC,则$\frac{b}{c}$的值为( )
| A. | $1+\sqrt{6}$ | B. | $1+2\sqrt{2}$ | C. | $1+3\sqrt{2}$ | D. | $1+3\sqrt{3}$ |
8.“x=1”是“(x-1)(x-2)=0”的( )
| A. | 必要但不充分条件 | B. | 充分但不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
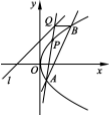 过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.
过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.