题目内容
12.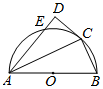 已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.
已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.(Ⅰ)求证:AD⊥CD;
(Ⅱ)若AB=5,DE=1,求AE的长.
分析 (Ⅰ)连接OC,则OC⊥CD,由OA=OC可得∠OAC=∠OCA,即可得到∠DAC=∠OCA,再根据平行线的性质即可得到结果;
(Ⅱ)连接CE,证得△DEC~△CBA,求出DC,根据切割线定理即可求得结果.
解答 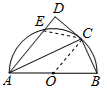 (Ⅰ)证明:连接OC,则OC⊥CD.
(Ⅰ)证明:连接OC,则OC⊥CD.
∵OA=OC,
∴∠OAC=∠OCA,
又∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∴AD⊥CD.
(Ⅱ)连接CE,∵AC平分∠BAD,
∴EC=CB,
∵∠DEC=∠CBA,
∴△DEC~△CBA,
∴$\frac{DE}{CB}=\frac{EC}{AB}$,
∴EC=$\sqrt{5}$,
∴DC=$\sqrt{E{C}^{2}-D{E}^{2}}$=2,
∵DC2=DE•DA,∴DA=4,
∴EA=3.
点评 本题考查圆的切线的性质,考查三角形相似的证明,考查切割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体的体积的最大值为( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
17.一抛物线形拱桥,当水面宽4米时,水面离拱顶2米,若水面下降1米,则水面的宽为( )
| A. | $\sqrt{6}$米 | B. | 2$\sqrt{6}$米 | C. | 6米 | D. | 8米 |