题目内容
画出函数y=-(x-3)|x|的图象,
(1)并根据图象写出函数的单调区间,以及在各单调区间上,函数是增函数还是减函数.
(2)若方程-(x-3)|x|=m与x轴有三个交点,求实数m的取值范围.
(1)并根据图象写出函数的单调区间,以及在各单调区间上,函数是增函数还是减函数.
(2)若方程-(x-3)|x|=m与x轴有三个交点,求实数m的取值范围.
考点:函数的图象,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)分两种情况去掉绝对值:
当x≥0时,y=-x(x-3);当x<0时,y=x(x-3),这两者都是抛物线的方程,画出抛物线后根据x的限制取舍相应的部分;
(2)构造函数y=m与函数y=-(x-3)|x|,使函数y=m与函数y=-(x-3)|x|有三个交点,求出m的范围.
当x≥0时,y=-x(x-3);当x<0时,y=x(x-3),这两者都是抛物线的方程,画出抛物线后根据x的限制取舍相应的部分;
(2)构造函数y=m与函数y=-(x-3)|x|,使函数y=m与函数y=-(x-3)|x|有三个交点,求出m的范围.
解答:
解:(1)当x≥0时,y=-x(x-3);当x<0时,y=x(x-3),这两个函数均为二次函数,
对称轴方程均为x=
,图象如下图:
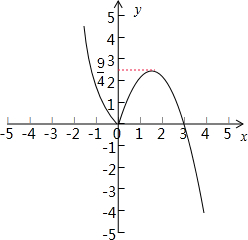
由图象可知,(-∞,0)为减区间,函数在此区间递减;
(0,
)为增区间,函数在此区间递增;
(
,+∞)为减区间,函数在此区间递减;
(2)方程-(x-3)|x|=m与x轴有三个交点,
函数y=m与函数y=-(x-3)|x|有三个交点,
从图象上可以看出m∈(0,
)
对称轴方程均为x=
| 3 |
| 2 |
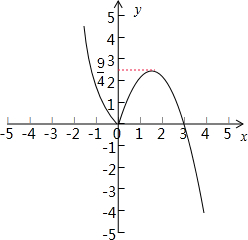
由图象可知,(-∞,0)为减区间,函数在此区间递减;
(0,
| 3 |
| 2 |
(
| 3 |
| 2 |
(2)方程-(x-3)|x|=m与x轴有三个交点,
函数y=m与函数y=-(x-3)|x|有三个交点,
从图象上可以看出m∈(0,
| 9 |
| 4 |
点评:带有绝对值符号的函数表达式,要分情况去掉绝对值符号,另外,方程的根的问题可转化为两函数图象的交点问题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数f(x)=
,则f(5)=( )
|
| A、32 | ||
| B、16 | ||
C、
| ||
D、
|