题目内容
17.已知a,b∈R,ab>0,则下列不等式中不正确的是( )| A. | |a+b|≥a-b | B. | $2\sqrt{ab}≤|{a+b}|$ | C. | |a+b|<|a|+|b| | D. | $|{\frac{b}{a}+\frac{a}{b}}|≥2$ |
分析 根据不等式的性质和基本不等式判断即可.
解答 解:对于A:∵ab>0,当a>0,b>0时,|a+b|=a+b≥a-b,当a<0,b<0时,|a+b|=-a-b≥a-b,故A成立,
对于B:当ab>0,∴(a+b)2=a2+b2+2ab≥4ab,故B成立,
对于C:a>0,b>0时,或a<0,b<0,时|a+b|=|a|+|b|,故C不正确,
对于D:ab>0,∴|$\frac{b}{a}$+$\frac{a}{b}$|=$\frac{b}{a}$+$\frac{a}{b}$≥2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=2,当且仅当a=b时取等号,故D成立
故选:C
点评 本题考查了不等式的性质和基本不等式的应用,属于基础题.

练习册系列答案
相关题目
5.已知复数$z=\frac{1+2i}{i}$,i为虚数单位.则z的虚部为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
12.如图是一个几何体的三视图,则这个几何体是( )


| A. | 四棱锥 | B. | 圆锥 | C. | 三棱锥 | D. | 三棱台 |
2.设a,b∈R,则“a+b>4”是“a>2且b>2”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.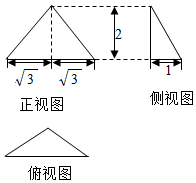 已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
 已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )| A. | 20π | B. | 16π | C. | 8π | D. | 17π |