题目内容
16.过点(1,1)且与曲线y=x3相切的切线方程为( )| A. | y=3x-2 | B. | y=$\frac{3}{4}$x+$\frac{1}{4}$ | ||
| C. | y=3x-2或y=$\frac{3}{4}$x+$\frac{1}{4}$ | D. | y=3x-2或y=$\frac{3}{4}$x-$\frac{1}{4}$ |
分析 设切点为(x0,y0),根据解析式求出导数、y0,由导数的几何意义求出切线的斜率,由点斜式方程求出切线方程,把点(1,1)代入切线方程通过因式分解求出x,代入切线方程化简即可.
解答 解:(1)设切点为(x0,y0),由题意得y=3x2,y0=x03,
则切线的斜率k=3x02,
∴切线方程是:y-x03=3x02(x-x0),①
∵切线过点(1,1),∴1-x03=3x02(1-x0),
化简得,2x03-3x02+1=0,
2(x03-1)-3(x02-1)=0,
则(x0-1)(2x02-x0-1)=0,
解得x0=1或x0=-$\frac{1}{2}$,代入①得:3x-y-2=0或3x-4y+1=0,
∴切线方程为3x-y-2=0或3x-4y+1=0.
故选:C.
点评 本题考查了导数的几何意义,即点P处的切线的斜率是该点出的导数值,以及切点在曲线上和切线上的应用,注意在某点处的切线和过某点的切线的区别,考查化简、计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.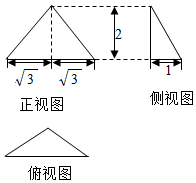 已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
 已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )| A. | 20π | B. | 16π | C. | 8π | D. | 17π |
4.设集合A={x|x<3},$B=\left\{{x\left|{\frac{x-1}{x-4}≤0}\right.}\right\}$,则(∁RA)∩B=( )
| A. | (1,3) | B. | (3,4) | C. | [1,3] | D. | [3,4) |
1.已知△ABC的顶点B,C在椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC上,则△ABC的周长是( )
| A. | 8 | B. | 8$\sqrt{3}$ | C. | 16 | D. | 24 |