某商店每双皮鞋的进货价为80元.根据以往经验.以每双90元销售时.每月能卖出400双.而每加价1元或减价1元销售时.每月销量会减少或增加20双.为了每月获取最大利润.商店应如何定价?每月的最大利润为多少? 题目和参考答案——青夏教育精英家教网—

题目内容

4．某商店每双皮鞋的进货价为80元，根据以往经验，以每双90元销售时，每月能卖出400双，而每加价1元或减价1元销售时，每月销量会减少或增加20双，为了每月获取最大利润，商店应如何定价？每月的最大利润为多少？

分析假设售价在90元的基础上涨x元，从而得到销售量，进而可以构建函数关系式，利用二次函数求最值的方法求出函数的最值．

解答解：设售价在90元的基础上涨或减价x元，因为这种商品每个涨价或减价1元，其销售量就减少或增加20个，所以若涨或减价x元，则销售量减少或增加20x
则按90+x元售出时，能售出400-20x个，每个的利润是90+x-80=10+x元
设总利润为y元，则y=（10+x）（400-20x）=-20x²+200x+4000，对称轴为x=5，定义域为（0≤x＜20），
所以x=5时，y有最大值，售价则为95元，
所以售价定为每个95元时，利润最大，每月的最大利润为4500元．

点评本题以实际问题为载体，考查函数模型的构建，考查利用数学知识解决实际问题，解题的关键是构造利润函数．

练习册系列答案

15．设函数$f（x）=sin（2x-\frac{π}{2}），x∈R$，则f（x）是（　　）

	A．	最小正周期为π的奇函数		B．	最小正周期为$\frac{π}{2}$的偶函数
	C．	最小正周期为$\frac{π}{2}$的奇函数		D．	最小正周期为π的偶函数

12．求下列表达式的值
（1）$\frac{（{a}^{\frac{2}{3}}•{b}^{-1}）^{-\frac{1}{2}}•{a}^{\frac{1}{2}}•{b}^{\frac{1}{3}}}{\root{6}{a•{b}^{5}}}$（a＞0，b＞0）
（2）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$．

19．

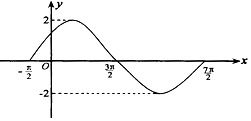已知f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）在一个周期内图象如图所示．
（1）试确定A，ω，φ的值．
（2）求y=$\sqrt{3}$与函数f（x）的交点坐标．

9．

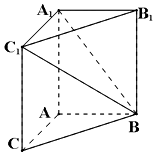如图，在三棱柱ABC-A₁B₁C₁中，AA₁C₁C是边长为的正方形，平面ABC⊥平面AA₁C₁C，AB=3，BC=5．
（1）求证：AA₁⊥平面ABC；
（2）求二面角A₁-BC₁-B₁的余弦值；
（3）在线段BC₁上是否存在点D，使得AD⊥A₁B？若存在，求出$\frac{BD}{B{C}_{1}}$的值，若不存在，说明理由．

16．已知函数f（x）=$\frac{1-x}{ax}$+lnx，且a＞0
（1）若函数f（x）在[1，+∞）上是增函数，求a的取值范围；
（2）当a=1时，求函数f（x）在[1，e]的最大值和最小值．

13．已知函数$f（x）=\sqrt{-{x^2}+2x+8}$的定义域为集合A，函数g（x）=lg（-x²+6x+m）的定义域为集合B．
（1）当m=-5时，求A∩∁_UB；
（2）若A∩B={x|-1＜x≤4}，求实数m的值．

14．已知，△ABC中，A（1，1），B（2，-3），C（3，5），写出满足下列条件的直线方程（要求最终结果都用直线的一般式方程表示，其他形式的结果不得分．）
（1）求直线AB方程；
（2）BC边中点D，求中线AD方程；
（3）BC边上的高线的方程；
（4）BC边的垂直平分线的方程．

试题分类