题目内容
 已知在平面直角坐标系中,坐标原点为O,点A,B在x轴上,OA=1,OB=5,点C在y轴上,OC=2.5,第一象限有一点D的坐标为(3,4),连接AD,BD,点E是线段AB上一动点(不与点A重合),过E作EF⊥AB交射线AD于点F,以EF为一边在EF的右侧作正方形EFGH,设E点的坐标为(t,0)
已知在平面直角坐标系中,坐标原点为O,点A,B在x轴上,OA=1,OB=5,点C在y轴上,OC=2.5,第一象限有一点D的坐标为(3,4),连接AD,BD,点E是线段AB上一动点(不与点A重合),过E作EF⊥AB交射线AD于点F,以EF为一边在EF的右侧作正方形EFGH,设E点的坐标为(t,0)(1)求射线AD的解析式;
(2)在线段AB上是否存在点E,使△OCG为等腰三角形?若存在,求正方形EFGH的边长;若不存在,请说明理由;
(3)设正方形EFGH与△ABD重叠部分面积为S,求S与t的函数关系式.
考点:直线的一般式方程,函数解析式的求解及常用方法
专题:数形结合,分类讨论,函数的性质及应用
分析:(1)根据点A、D的坐标求出射线AD的方程,注意x的取值范围;
(2)根据等腰三角形的定义讨论CO=OG、CG=OG和CG=OG时,t的值是什么,求出对应的正方形边长即可;
(3)分0<t≤
,
<t≤2,2<t≤3,3<t≤5,-1<t≤0几种情况,讨论S的解析式是什么,从而得出S与t的函数关系式.
(2)根据等腰三角形的定义讨论CO=OG、CG=OG和CG=OG时,t的值是什么,求出对应的正方形边长即可;
(3)分0<t≤
| 7 |
| 5 |
| 7 |
| 5 |
解答:
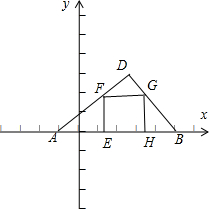 解:(1)∵点A(-1,0),D(3,4),
解:(1)∵点A(-1,0),D(3,4),
∴射线AD的方程是
=
,即x-y+1=0(x≥-1);
(2)由(1)知,y=x+1(x≥-1),
当x=0时,y=1;
∵E(t,0),∴OE=t(-1<t≤5),
∴AE=t+1,EF=t+1;
∵四边形EFGH是正方形,
∴EF=FG=GH=HE=t+1;
∴G(2t+1,t+1);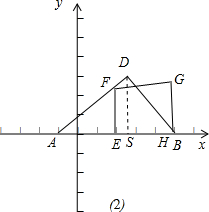
①当CO=OG时,(2t+1)2+(t+1)2=2.52,
解得t1=0.5,t2=-1.7(舍去),
∴正方形的边长为0.5+1=1.5;
②当CG=OG时,(2t+1)2+(t+1-2.5)2=2.52,
解得t1=
,t2=
(舍去),
∴正方形的边长为
+1=
;
③当CG=OG时,(2t+1)2+(t+1)2=(2t+1)2+(t+1-2.5)2,
解得t=0.25,
∴正方形的边长为0.25+1=1.25;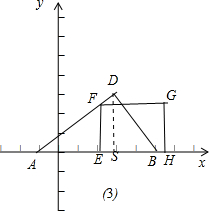
综上,存在点E,使△OCG为等腰三角形,此时正方形EFGH的边长为1.5,或
,或1.25;
(3)设BD的方程为y=kx+b,∵B(5,0),D(3,4),
∴
解得k=-2、b=10;
∴直线BD:y=-2x+10,
把G点的坐标代入得,t+1=-2(2t+1)+10,解得t=
;
①如图(1),当0<≤
时,S=(t+1)2=t2+2t+1;
②如图(2),当点H与点B重合时,即2t+1=5,t=2时,
令t+1=-2x+10,得x=4.5-
t;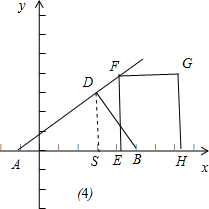
∴当
<t≤2时,S=
(4.5-
t-t+5-t)(t+1)-
•2(4-2t)(4-2t)=-
t2+
t-
;
③如图(3),当2<t≤3时,S=
(4.5-
t-t+5)(t+1)=-
t2+
t+
;
④如图(4),作DS⊥OB于S,∴∠DSB=90°,∴OS=3,DS=4,OB=5,
∴BS=2,∴tan∠DBS=2;
当3<t≤5时,BE=5-t,PE=2(5-t),
∴S=
×2(5-t)(5-t)=t2-10t+25;
⑤如图(5),当-1<t≤0时,E(t,0),OE=-t,∴AE=EF=1+t,
∴S=(t+1)2=t2+2t+1;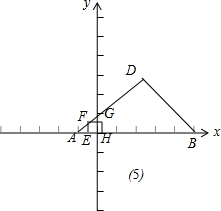
综上,S与t的函数关系式是S(t)=
.
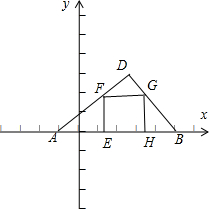 解:(1)∵点A(-1,0),D(3,4),
解:(1)∵点A(-1,0),D(3,4),∴射线AD的方程是
| y-0 |
| 4-0 |
| x+1 |
| 3+1 |
(2)由(1)知,y=x+1(x≥-1),
当x=0时,y=1;
∵E(t,0),∴OE=t(-1<t≤5),
∴AE=t+1,EF=t+1;
∵四边形EFGH是正方形,
∴EF=FG=GH=HE=t+1;
∴G(2t+1,t+1);

①当CO=OG时,(2t+1)2+(t+1)2=2.52,
解得t1=0.5,t2=-1.7(舍去),
∴正方形的边长为0.5+1=1.5;
②当CG=OG时,(2t+1)2+(t+1-2.5)2=2.52,
解得t1=
| ||
| 10 |
-
| ||
| 10 |
∴正方形的边长为
| ||
| 10 |
| ||
| 10 |
③当CG=OG时,(2t+1)2+(t+1)2=(2t+1)2+(t+1-2.5)2,
解得t=0.25,
∴正方形的边长为0.25+1=1.25;
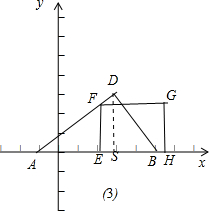
综上,存在点E,使△OCG为等腰三角形,此时正方形EFGH的边长为1.5,或
| ||
| 10 |
(3)设BD的方程为y=kx+b,∵B(5,0),D(3,4),
∴
|
∴直线BD:y=-2x+10,
把G点的坐标代入得,t+1=-2(2t+1)+10,解得t=
| 7 |
| 5 |
①如图(1),当0<≤
| 7 |
| 5 |
②如图(2),当点H与点B重合时,即2t+1=5,t=2时,
令t+1=-2x+10,得x=4.5-
| 1 |
| 2 |

∴当
| 7 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |
| 4 |
| 39 |
| 2 |
| 45 |
| 4 |
③如图(3),当2<t≤3时,S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
| 19 |
| 4 |
④如图(4),作DS⊥OB于S,∴∠DSB=90°,∴OS=3,DS=4,OB=5,
∴BS=2,∴tan∠DBS=2;
当3<t≤5时,BE=5-t,PE=2(5-t),
∴S=
| 1 |
| 2 |
⑤如图(5),当-1<t≤0时,E(t,0),OE=-t,∴AE=EF=1+t,
∴S=(t+1)2=t2+2t+1;
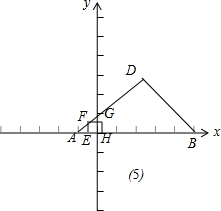
综上,S与t的函数关系式是S(t)=
|
点评:本题考查了分段函数的应用问题,也考查了数形结合思想的应用问题,考查了等腰三角形的应用问题,考查了分类讨论思想的应用问题,考查了多边形的面积的计算问题,是综合性题目.

练习册系列答案
相关题目
在抛物线y2=8x中,以(1,-1)为中点的弦所在的直线方程为( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
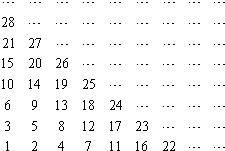 将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=
将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=