题目内容
已知函数f(x)=alnx-x2.
(1)当a=2时,求函数y=f(x)在区间[
,2]上的最大值;
(2)令g(x)=f(x)+ax,若y=g(x)在(0,3)不单调,求a的取值范围.
(1)当a=2时,求函数y=f(x)在区间[
| 1 |
| 2 |
(2)令g(x)=f(x)+ax,若y=g(x)在(0,3)不单调,求a的取值范围.
考点:利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的综合应用
分析:(1)由导函数值的正负得到函数的单调性和最值情况,从而得到本题结论;
(2)由题意y=g(x)在(0,3)不单调,知道在区间(0,3)内导函数的异号,对应方程有根在区间(0,3)内,得到相应有关系式,解不等式得到本题结论.
(2)由题意y=g(x)在(0,3)不单调,知道在区间(0,3)内导函数的异号,对应方程有根在区间(0,3)内,得到相应有关系式,解不等式得到本题结论.
解答:
解:(1)当a=2时,
函数f(x)=2lnx-x2,
∴f′(x)=
-2x=
=
,(x>0).
∴当
<x<1时,f′(x)>0,f(x)单调递增;
当1<x<2时,f′(x)<0,f(x)单调递减.
当x=1时,f′(x)=0,f(x)有极大值f(1)=-1.
∴函数y=f(x)在区间[
,2]上的最大值为-1.
(2)∵g(x)=f(x)+ax,
∴g(x)=alnx-x2+ax,
∴g′(x)=
-2x+a=
.
∵y=g(x)在(0,3)不单调,
∴g′(x)=0在区间(0,3)内异号,
∴方程-2x2+ax+a=0有两个不相等的实数根,且有根在区间(0,3)内.
∴记h(x)=2x2-ax-a,
由h(0)•h(3)<0得:0<a<
;
由
知,此时无解;
由h(0)=0得a=0,h(x)=2x2,不合题意;
由h(3)=0得a=
,h(x)=2x2-
x-
=
(x-3)(4x+3),不合题意.
综上,0<a<
.
∴a的取值范围是(0,
).
函数f(x)=2lnx-x2,
∴f′(x)=
| 2 |
| x |
| 2-2x2 |
| x |
| -2(x+1)(x-1) |
| x |
∴当
| 1 |
| 2 |
当1<x<2时,f′(x)<0,f(x)单调递减.
当x=1时,f′(x)=0,f(x)有极大值f(1)=-1.
∴函数y=f(x)在区间[
| 1 |
| 2 |
(2)∵g(x)=f(x)+ax,
∴g(x)=alnx-x2+ax,
∴g′(x)=
| a |
| x |
| -2x2+ax+a |
| x |
∵y=g(x)在(0,3)不单调,
∴g′(x)=0在区间(0,3)内异号,
∴方程-2x2+ax+a=0有两个不相等的实数根,且有根在区间(0,3)内.
∴记h(x)=2x2-ax-a,
由h(0)•h(3)<0得:0<a<
| 9 |
| 2 |
由
|
由h(0)=0得a=0,h(x)=2x2,不合题意;
由h(3)=0得a=
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
综上,0<a<
| 9 |
| 2 |
∴a的取值范围是(0,
| 9 |
| 2 |
点评:本题考查了函数的最值和导函数的知识,本题难度适中,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在抛物线y2=8x中,以(1,-1)为中点的弦所在的直线方程为( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
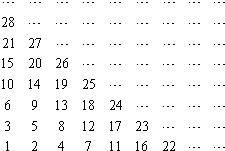 将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=
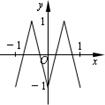
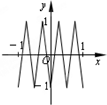
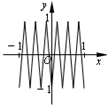
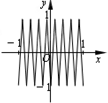
将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=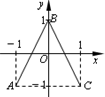 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )