题目内容
若函数f(x)满足?m∈R,m≠0,对定义域内的任意x,f(x+m)=f(x)+f(m)恒成立,则称f(x)为m函数,现给出下列函数:
①y=
;
②y=2x;
③y=sinx;
④y=1nx
其中为m函数的个数为( )
①y=
| 1 |
| x |
②y=2x;
③y=sinx;
④y=1nx
其中为m函数的个数为( )
| A、1 | B、3 | C、4 | D、2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据m函数定义逐项判断即可.
解答:
解:①若f(x)=
,则由f(x+m)=f(x)+f(m)得,
=
+
即
=
-
=
,
所以不存在常数m使f(x+m)=f(x)+f(m)成立,所以①不是m函数.
②若f(x)=2x,由f(x+m)=f(x)+f(m)得,2(x+m)=2x+2m,此时恒成立,所以②y=2x是m函数.
③若f(x)=sinx,由f(x+m)=f(x)+f(m)得sin(x+m)=sinx+sinm,所以当m=π时,f(x+m)=f(x)+f(m)成立,所以③y=sinx是m函数.
④若f(x)=1nx,则由f(x+m)=f(x)+f(m)得ln(x+m)=lnx+lnm,即ln(x+m)=lnmx,所以x+m=mx,要使x+m=mx成立则有
,所以方程无解,所以④y=1nx不是m函数.
所以为m函数的序号是②③.
其中为m函数的个数为:2个.
故选:D
| 1 |
| x |
| 1 |
| x+m |
| 1 |
| x |
| 1 |
| m |
| 1 |
| m |
| 1 |
| x+m |
| 1 |
| x |
| -m |
| x(x+m) |
所以不存在常数m使f(x+m)=f(x)+f(m)成立,所以①不是m函数.
②若f(x)=2x,由f(x+m)=f(x)+f(m)得,2(x+m)=2x+2m,此时恒成立,所以②y=2x是m函数.
③若f(x)=sinx,由f(x+m)=f(x)+f(m)得sin(x+m)=sinx+sinm,所以当m=π时,f(x+m)=f(x)+f(m)成立,所以③y=sinx是m函数.
④若f(x)=1nx,则由f(x+m)=f(x)+f(m)得ln(x+m)=lnx+lnm,即ln(x+m)=lnmx,所以x+m=mx,要使x+m=mx成立则有
|
所以为m函数的序号是②③.
其中为m函数的个数为:2个.
故选:D
点评:本题考查函数恒成立问题,考查学生利用所学知识分析解决新问题的能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若非零复数z1,z2满足|z1+z2|=|z1-z2|,则
与
所成的角为( )
| OZ1 |
| OZ2 |
| A、30° | B、45° |
| C、60° | D、90° |
设a、b、c表示三条直线,α、β表示两个平面,则下列命题中不正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
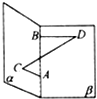 如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )
如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )