题目内容
设集合M={x|x=
+
,k∈Z},N={x|x=kπ±
,k∈Z},则M、N的关系是( )
| kπ |
| 2 |
| π |
| 4 |
| π |
| 4 |
| A、M=N | B、M≠N |
| C、M?N | D、M?N |
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:从元素满足的公共属性的结构入手,对集合M中的k分奇数和偶数讨论,从而可得两集合的关系.
解答:
解:对于集合M,当k=2m(m∈Z)时,x=mπ+
,m∈Z;
当k=2m-1(m∈Z)时,x=mπ-
,m∈Z,
∴M=N.
故选:A.
| π |
| 4 |
当k=2m-1(m∈Z)时,x=mπ-
| π |
| 4 |
∴M=N.
故选:A.
点评:本题的考点是集合的包含关系判断及应用,解题的关键是对集合M中的k分奇数和偶数讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若非零复数z1,z2满足|z1+z2|=|z1-z2|,则
与
所成的角为( )
| OZ1 |
| OZ2 |
| A、30° | B、45° |
| C、60° | D、90° |
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
已知定义域为R的函数y=f(x)在[0,7]上只有1和3两个零点,且y=f(2-x)与y=(7+x)都是偶函数,则函数y=f(x)在[-2013,2013]上的零点个数为( )
| A、804 | B、805 |
| C、806 | D、807 |
命题“对任意x∈R,都有2x>0”的否定是( )
| A、对任意x∈R,都有2x≤0 |
| B、不存在x∈R,使得2x≤0 |
| C、存在x0∈R,使得2x>0 |
| D、存在x0∈R,2x0≤0 |
有下列调查方式:
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
| A、分层抽样,系统抽样,简单随机抽样 |
| B、系统抽样,系统抽样,简单随机抽样 |
| C、分层抽样,简单随机抽样,简单随机抽样 |
| D、系统抽样,分层抽样,简单随机抽样 |
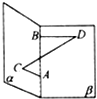 如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )
如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )