题目内容
直线l：y=k（x+2）被圆C：x2+y2=4截得的线段长为2，则k的值为（ ）
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
考点：直线与圆相交的性质
专题：直线与圆
分析：由已知条件得圆心C（0，0）到直线l：y=k（x+2）的距离为：
=
，由此能求出k．
| 22-12 |
| 3 |
解答：
解：∵直线l：y=k（x+2）被圆C：x2+y2=4截得的线段长为2，
∴圆心C（0，0）到直线l：y=k（x+2）的距离为：
=
，
∴
=
，解得k=±
．
故选：C．
∴圆心C（0，0）到直线l：y=k（x+2）的距离为：
| 22-12 |
| 3 |
∴
| |2k| | ||
|
| 3 |
| 3 |
故选：C．
点评：本题考查k的值的求法，是基础题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
相关题目
一个乒乓球队里有男队员5人，女队员4人，从中选出男、女队员各一名组成混合双打，不同的选法共有（ ）
| A、9种 | B、10种 |
| C、15种 | D、20种 |
设椭圆
+
=1（a＞b＞0）的两个焦点分别为F1，F2，点P在椭圆上，且
•
=0，tan∠PF1F2=
，则该椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
双曲线x2+
=1的实轴长是虚轴长的2倍，则m=（ ）
| y2 |
| m |
A、-
| ||
B、-
| ||
| C、-2 | ||
| D、-4 |
若非零复数z1，z2满足|z1+z2|=|z1-z2|，则
与
所成的角为（ ）
| OZ1 |
| OZ2 |
| A、30° | B、45° |
| C、60° | D、90° |
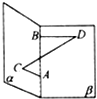如图，在120°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=5，AC=2，BD=3，则线段CD的长为（ ）