题目内容
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的数学期望.
(1)当红球与白球各2个时甲获胜的概率最大
(2)
【解析】
试题分析:(1)根据甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜,可得甲获胜的概率,再利用基本不等式,可得x,y的值;
(2)由题意知取出的3个球中红球个数ξ的取值为1,2,3,4,分别求出其发生的概率,进而求出次数ξ的数学期望
【解析】
(1)由题意, ;
;
∴ ,
,
当且仅当x=y=2时“=”成立
所以当红球与白球各2个时甲获胜的概率最大
(2)取出的3个球中红球个数ξ=0,1,2,3

 ,
,
所以

练习册系列答案
相关题目
 ,
,
 ,若
,若 ,则
,则 的最小值为
的最小值为 B.
B. C.
C. D.
D.
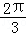 ,则线段AB的长度为( )
,则线段AB的长度为( ) C.2 D.2
C.2 D.2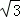
 C.
C. D.
D.
 ,要得到
,要得到 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位. B.向左平移
B.向左平移 D.向左平移
D.向左平移 B.
B. C.
C. D.
D.