题目内容
已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( )
A. B.
B. C.
C. D.
D.
A
【解析】
试题分析:设AB=1,则AA1=2,分别以 的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,设
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,设 =(x,y,z)为平面BDC1的一个法向量,CD与平面BDC1所成角为θ,
=(x,y,z)为平面BDC1的一个法向量,CD与平面BDC1所成角为θ,
则sinθ=| |,在空间坐标系下求出向量坐标,代入计算即可.
|,在空间坐标系下求出向量坐标,代入计算即可.
【解析】
设AB=1,则AA1=2,分别以 的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
如下图所示:

则D(0,0,2),C1(0,1,0),B(1,1,2),C(0,1,2),
 =(1,1,0),
=(1,1,0), =(0,1,﹣2),
=(0,1,﹣2), =(0,1,0),
=(0,1,0),
设 =(x,y,z)为平面BDC1的一个法向量,则
=(x,y,z)为平面BDC1的一个法向量,则 ,即
,即 ,取
,取 =(﹣2,2,1),
=(﹣2,2,1),
设CD与平面BDC1所成角为θ,则sinθ=| |=
|= ,
,
故选A.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 B.
B. C.
C. D.
D.
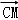 ,
, >的值为( )
>的值为( )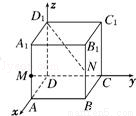
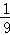 B.
B.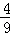
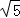 C.
C.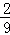
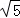 D.
D.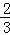
 = .
= . (
( 是虚数单位)的共轭复数为
是虚数单位)的共轭复数为 (B)
(B) (C)
(C) (D)
(D)
 的展开式中第3项的系数是
的展开式中第3项的系数是 ,数列
,数列
 是公差为
是公差为 的等差数列,且前
的等差数列,且前 项和为
项和为 ,则
,则 = .
= .