题目内容
设函数f(x)=|sin(x+
)|(x∈R),求f(x)的单调递增区间.
| π |
| 3 |
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:根据函数y=|sinx|的增区间,令kπ≤x+
≤kπ+
,k∈z,求得x的范围,可得f(x)的单调递增区间.
| π |
| 3 |
| π |
| 2 |
解答:
解:令kπ≤x+
≤kπ+
,k∈z,求得kπ-
≤x≤kπ+
,
可得函数f(x)的增区间为[kπ-
,kπ+
],k∈z.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
可得函数f(x)的增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查函数y=|sinx|的增区间,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知函数f(x)=loga(ax2-x+3)在[2,4]上是增函数,则实数a的取值范围是( )
| A、a>1 | ||||
| B、0<a<1或a>1 | ||||
C、
| ||||
D、
|
在1,2,3,4四个数中,任取两个不同的数,其和大于积的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知椭圆
已知椭圆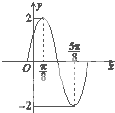 已知函数f(x)=Asin(ωx+φ)其中A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)其中A>0,ω>0,0<φ<