题目内容
19.在等比数列{an}中,已知${a_1}=\frac{1}{4},{a_3}{a_5}=4({{a_4}-1})$,则{an}的前10项和S10=$\frac{1023}{4}$.分析 由等比数列通项公式得公比q=2,由此能求出{an}的前10项和S10.
解答 解:∵在等比数列{an}中,${a_1}=\frac{1}{4},{a_3}{a_5}=4({{a_4}-1})$,
∴$\frac{1}{4}{q}^{2}•\frac{1}{4}{q}^{4}$=4($\frac{1}{4}{q}^{3}-1$),
解得q=2,
{an}的前10项和S10=$\frac{{a}_{1}(1-{q}^{10})}{1-q}$=$\frac{\frac{1}{4}(1-{2}^{10})}{1-2}$=$\frac{1023}{4}$.
故答案为:$\frac{1023}{4}$.
点评 本题考查等比数列前10项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
9.直线$\sqrt{3}$x-y+3=0的倾斜角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 150° |
10.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x+2y-4≤0}\\{3x+y-3≥0}\\{x-y-1≤0}\end{array}}\right.$,则目标函数z=x-2y的最小值为( )
| A. | $-\frac{16}{5}$ | B. | -3 | C. | 0 | D. | 1 |
14.已知向量$\overrightarrow{a}$=(cos40°,sin40°),$\overrightarrow{b}$=(sin20°,cos20°),$\overrightarrow{u}$=$\sqrt{3}$$\overrightarrow{a}$+λ$\overrightarrow{b}$(其中λ∈R),则|$\overrightarrow{u}$|的最小值为( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
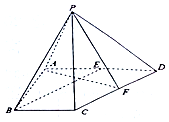 如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.
如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.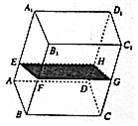 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: