题目内容
9．
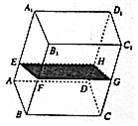如图，在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：①水的部分始终呈棱柱状；
②水面四边形EFGH的面积不改变；
③棱A1D1始终与水面EFGH平行；
④当E∈AA1时，AE+BF是定值．其中正确说法的是（ ）
| A． | ②③④ | B． | ①②④ | C． | ①③④ | D． | ①②③ |
分析 ①水的部分始终呈棱柱状；从棱柱的特征平面判断即可；
②水面四边形EFGH的面积不改变；可以通过EF 的变化EH不变判断正误；
③棱A1D1始终与水面EFGH平行；利用直线与平面平行的判断定理，推出结论；
④当E∈AA1时，AE+BF是定值．通过水的体积判断即可．
解答 解：①水的部分始终呈棱柱状；从棱柱的特征平面AA1B1B平行平面CC1D1D即可判断①正确；
②水面四边形EFGH的面积不改变；EF是可以变化的EH不变的，所以面积是改变的，②是不正确的；
③棱A1D1始终与水面EFGH平行；由直线与平面平行的判断定理，可知A1D1∥EH，所以结论正确；
④当E∈AA1时，AE+BF是定值．水的体积是定值，高不变，所以底面面积不变，所以正确．
故选：C．
点评 本题是基础题，考查棱柱的结构特征，直线与平面平行的判断，棱柱的体积等知识，考查计算能力，逻辑推理能力．
练习册系列答案
相关题目
20．圆O的半径为定长，A是平面上一定点，P是圆上任意一点，线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹为（ ）
| A． | 一个点 | B． | 椭圆 | ||
| C． | 双曲线 | D． | 以上选项都有可能 |
4．下列叙述中错误的是（ ）
| A． | 若点P∈α，P∈β且α∩β=l，则P∈l | |
| B． | 三点A，B，C能确定一个平面 | |
| C． | 若直线a∩b=A，则直线a与b能够确定一个平面 | |
| D． | 若点A∈l，B∈l，且A∈α，B∈α，则l?α |
1．已知$f（x）=\left\{\begin{array}{l}{log_a}（{a{x^2}-4x+4}），x≥1\\（{3-a}）x+b，x≤1\end{array}\right.$在（-∞，+∞）上满足$\frac{{f（{x_2}）-f（{x_1}）}}{{{x_2}-{x_1}}}＞0$，则b的取值范围是（ ）
| A． | （-∞，0） | B． | [1，+∞） | C． | （-1，1） | D． | [0，1） |
18．已知随机变量X～B（n，$\frac{1}{3}$），若D（x）=$\frac{4}{3}$，则P（X=2）=（ ）
| A． | $\frac{13}{15}$ | B． | $\frac{2}{81}$ | C． | $\frac{13}{243}$ | D． | $\frac{80}{243}$ |
19．已知A（x，-2），B（3，0），若直线AB的斜率为2，则x的值为（ ）
| A． | -1 | B． | 2 | C． | -1或2 | D． | -2 |