题目内容
设函数f(x)=|2x+1|-|x-3|.
(1)求函数y=f(x)的最小值;
(2)若f(x)≥ax+
-
恒成立,求实数a的取值范围.
(1)求函数y=f(x)的最小值;
(2)若f(x)≥ax+
| a |
| 2 |
| 7 |
| 2 |
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(1)去绝对值,分三段,写出函数表达式,判断各段的单调性,得到最小值.
(2)令g(x)=ax+
-
,画出f(x)、g(x)的图象,通过直线过点(-
,-
),旋转观察,即可得到a的取值范围.
(2)令g(x)=ax+
| a |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
解答:
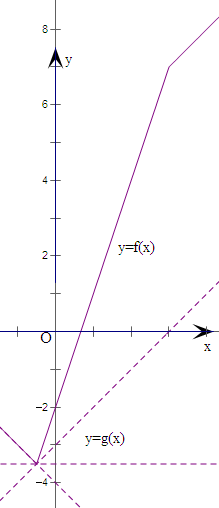 解:(1)函数f(x)=|2x+1|-|x-3|=
解:(1)函数f(x)=|2x+1|-|x-3|=
,
故函数的减区间为(-∞,-
)、增区间为(-
,+∞),
故当x=-
时,函数f(x)取得最小值为-
.
(2)由于函数g(x)=ax+
-
恒过定点(-
,-
),若f(x)≥ax+
-
恒成立,
则由图象可知-1≤a≤1.
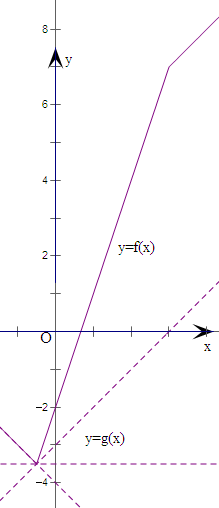 解:(1)函数f(x)=|2x+1|-|x-3|=
解:(1)函数f(x)=|2x+1|-|x-3|=
|
故函数的减区间为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
故当x=-
| 1 |
| 2 |
| 7 |
| 2 |
(2)由于函数g(x)=ax+
| a |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| a |
| 2 |
| 7 |
| 2 |
则由图象可知-1≤a≤1.
点评:本题考查绝对值函数的最值,注意写成分段函数的形式,讨论各段的单调性,从而求出最值,考查分段函数的图象和运用,不等式的恒成立问题转化为图象的位置关系,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
设全集U=R,A={x|x≤1+
,x∈R },B={1,2,3,4},则B∩∁UA=( )
| 2 |
| A、{4} |
| B、{3,4} |
| C、{2,3,4} |
| D、{1,2,3,4} |
设M是△ABC所在平面上的一点,且
+
+
=
,D是AC中点,则
的值为( )
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
|
| ||
| |BM| |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、(x-1)2+y2=16 |
| D、x2+(y-1)2=16 |
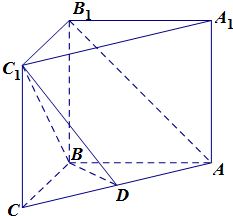 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=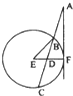 如图,过圆E外一点A作一条直线与圆E交与B,且AB=
如图,过圆E外一点A作一条直线与圆E交与B,且AB=