题目内容
设二次函数f(x)=ax2+bx+c(a,b∈R)满足条件:①当x∈R时,f(x)的最大值为0,且f(x-1)=f(3-x)成立;②二次函数f(x)的图象与直线y=-2交于A、B两点,且|AB|=4
(Ⅰ)求f(x)的解析式;
(Ⅱ)求最小的实数n(n<-1),使得存在实数t,只要当x∈[n,-1]时,就有f(x+t)≥2x成立.
(Ⅰ)求f(x)的解析式;
(Ⅱ)求最小的实数n(n<-1),使得存在实数t,只要当x∈[n,-1]时,就有f(x+t)≥2x成立.
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)根据题意可假设f(x)=a(x-1)2.(a<0),令a(x-1)2=-2,x=1±
,求解即可得出解析式.
(Ⅱ)利用不等式解得-t-1-2
≤x≤-t-1+2
,又f(x+t)≥2x在x∈[n,-1]时恒成立,转化为令g(t)=-t-1-2
,易知g(t)=-t-1-2
单调递减,
所以,g(t)≥g(4)=-9,得出n能取到的最小实数为-9.
|
(Ⅱ)利用不等式解得-t-1-2
| t |
| t |
| t |
| t |
所以,g(t)≥g(4)=-9,得出n能取到的最小实数为-9.
解答:
解:(Ⅰ)由f(x-1)=f(3-x)可知函数f(x)的对称轴为x=1,
由f(x)的最大值为0,可假设f(x)=a(x-1)2.(a<0)
令a(x-1)2=-2,x=1±
,则易知2
=4,a=-
.
所以,f(x)=-
(x-1)2.
(Ⅱ)由f(x+t)≥2x可得,-
(x-1+t)2≥2x,即x2+2(t+1)x+(t-1)2≤0,
解得-t-1-2
≤x≤-t-1+2
,
又f(x+t)≥2x在x∈[n,-1]时恒成立,
可得由(2)得0≤t≤4.
令g(t)=-t-1-2
,易知g(t)=-t-1-2
单调递减,
所以,g(t)≥g(4)=-9,
由于只需存在实数,故n≥-9,则n能取到的最小实数为-9.
此时,存在实数t=4,只要当x∈[n,-1]时,就有f(x+t)≥2x成立.
由f(x)的最大值为0,可假设f(x)=a(x-1)2.(a<0)
令a(x-1)2=-2,x=1±
|
|
| 1 |
| 2 |
所以,f(x)=-
| 1 |
| 2 |
(Ⅱ)由f(x+t)≥2x可得,-
| 1 |
| 2 |
解得-t-1-2
| t |
| t |
又f(x+t)≥2x在x∈[n,-1]时恒成立,
可得由(2)得0≤t≤4.
令g(t)=-t-1-2
| t |
| t |
所以,g(t)≥g(4)=-9,
由于只需存在实数,故n≥-9,则n能取到的最小实数为-9.
此时,存在实数t=4,只要当x∈[n,-1]时,就有f(x+t)≥2x成立.
点评:本题考查了函数的解析式的求解,方程组求解问题,分类讨论求解,属于中档题.

练习册系列答案
相关题目
已知数列{an}是等差数列,若a2+2,a4+4,a6+6构成等比数列,这数列{an}的公差d等于( )
| A、1 | B、-1 | C、2 | D、-2 |
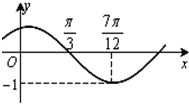 函数f(x)=sin(ωx+φ)(其中|φ|<
函数f(x)=sin(ωx+φ)(其中|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
以原点O为中心,焦点在x轴上的双曲线C,有一条渐近线的倾斜角为60°,点F是该双曲线的右焦点.位于第一象限内的点M在双曲线C上,且点N是线段MF的中点.若|
|=|
|+1,则双曲线C的方程为( )
| ON |
| NF |
A、x2-
| ||||
B、x2-
| ||||
C、
| ||||
| D、3x2-y2=1 |