题目内容
15.已知实数x,y满足条件$\left\{\begin{array}{l}x-y+3≥0\\ 2x+y-4≥0\\ x≤3\end{array}\right.$则z=x2+(y+1)2的最小值为5.分析 先根据条件画出可行域,z=x2+(y+1)2,再利用几何意义求最值,只需求出可行域内的点到点B(0,-1)距离的最值,从而得到z最值即可.
解答  解:先根据实数x,y满足条件$\left\{\begin{array}{l}x-y+3≥0\\ 2x+y-4≥0\\ x≤3\end{array}\right.$画出可行域,
解:先根据实数x,y满足条件$\left\{\begin{array}{l}x-y+3≥0\\ 2x+y-4≥0\\ x≤3\end{array}\right.$画出可行域,
z=x2+(y+1)2,
表示可行域内点B到A(0,-1)距离的平方,
当z是点A到直线2x+y-4=0的距离的平方时,z最小,
最小值为d2=$(\frac{0-1-4}{\sqrt{{2}^{2}+{1}^{2}}})^{2}$=5,
给答案为:5.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6.在复平面内,复数z的对应点为(1,2),复数z的共轭复数为( )
| A. | 1+2i | B. | 1-2i | C. | -2+i | D. | -2-i |
10.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)过点$(\sqrt{2},2\sqrt{2})$,过点(0,-2)的直线l与双曲线C的一条渐进线平行,且这两条平行线间的距离为$\frac{2}{3}$,则双曲线C的实轴长为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
7.已知复数z满足(3-i)z=2+i(i为虚数单位),则z的共轭复数是( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}i$ | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
4.已知实数a,b满足(a+2i)•bi=3i+6(i为虚数单位)则在复平面内,复数z=a+bi所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
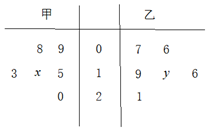 如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.
如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.