题目内容
已知函数f（x）=ax2+bx+c（a≠0）的图象过点A（0，1）和B（-1，0），且b2-4a≤0．求f（x）的解析式．
考点：二次函数的性质
专题：函数的性质及应用
分析：由题设，得f（0）=1，f（-1）=0，c=1，b=a+1，代入b2-4a≤0，得（a+1）2-4a≤0，即（a-1）2≤0，解得a=1，b=2．即可求出解析式．
解答：
解：∵函数f（x）=ax2+bx+c（a≠0）的图象过点A（0，1）和B（-1，0），
∴得f（0）=1，f（-1）=0，
求得：c=1，b=a+1．
∵b2-4a≤0，
∴得（a+1）2-4a≤0，即（a-1）2≤0，
解得a=1，b=2．
所以f（x）=x2+2x+1．
∴得f（0）=1，f（-1）=0，
求得：c=1，b=a+1．
∵b2-4a≤0，
∴得（a+1）2-4a≤0，即（a-1）2≤0，
解得a=1，b=2．
所以f（x）=x2+2x+1．
点评：本题考查了二次函数的性质，结合不等式求解，属于中档题，难度不大．
练习册系列答案
相关题目
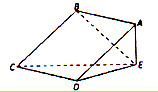如图所示四棱锥E-ABCD中，四边形ABCD为正方形，AE⊥平面CDB，且AR=3，