题目内容
已知二次函数f(x)=2x2+ax+b为偶函数,g(x)=(
-1)x+m,h(x)=c(x+1)2(c≠2),关于x的方程f(x)=h(x)有且仅有一根
.
(Ⅰ)求a,b,c的值;
(Ⅱ)若对任意的x∈[-1,1],
≤g(|x|)恒成立,求实数m的取值范围;
(Ⅲ)令φ(x)=
+
,若存在x1,x2∈[0,1]使得|φ(x1)-φ(x2)|≥g(m),求实数m的取值范围.
| 3 |
| 1 |
| 2 |
(Ⅰ)求a,b,c的值;
(Ⅱ)若对任意的x∈[-1,1],
| f(x) |
(Ⅲ)令φ(x)=
| f(x) |
| f(1-x) |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)由f(x)=f(-x)求a的值,再由关于x的方程f(x)=h(x)有且仅有一根
列式求得b,c的值;
(Ⅱ)把(Ⅰ)中求得的a代入f(x),求出当x=0时
≤g(|x|)恒成立的m的取值范围,然后验证对于任意的x∈[-1,1],
≤g(|x|)恒成立得到m的取值范围;
(Ⅲ)把存在x1,x2∈[0,1]使得|φ(x1)-φ(x2)|≥g(m)成立转化为|φ(x1)-φ(x2)|max≥
m,结合f(x)=2x2+1≥
(x+1)2在x∈[0,1]上恒成立变形可得
(x+1)≤
≤(
-1)x+1在x∈[0,1]上恒成立.进一步得到
(x+1)+
(1-x+1)≤φ(x)≤(
-1)x+1+(
-1)(1-x)+1,求得|φ(x1)-φ(x2)|的最大值后代入|φ(x1)-φ(x2)|max≥
m,即可求得m的取值范围.
| 1 |
| 2 |
(Ⅱ)把(Ⅰ)中求得的a代入f(x),求出当x=0时
| f(x) |
| f(x) |
(Ⅲ)把存在x1,x2∈[0,1]使得|φ(x1)-φ(x2)|≥g(m)成立转化为|φ(x1)-φ(x2)|max≥
| 3 |
| 2 |
| 3 |
| ||
| 3 |
| f(x) |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
解答:
解:(Ⅰ)∵二次函数f(x)=2x2+ax+b为偶函数,由f(x)=f(-x),得2(-x)2-ax+b=2x2+ax+b,即a=0,
由f(x)=h(x),可得(c-2)x2+2cx+c-b=0,代入x=
得:b=
c-
①,
由△=0,得c2=(c-2)(c-b) ②.
联立①②解得:b=1,c=
,
∴a=0,b=1,c=
;
(Ⅱ)f(x)=2x2+1,g(x)=(
-1)x+m,
当x=0时,由
≤g(|x|)恒成立,得m≥1;
当m=1时,(
)2-[(
-1)|x|+1]2=2(
-1)x2-2(
-1)|x|=2(
-1)|x|(|x|-1)≤0,
∴
≤(
-1)|x|+1,
∴对任意的x∈[-1,1],
≤g(|x|)恒成立的实数m的取值范围是[1,+∞);
(Ⅲ)由题意可知,|φ(x1)-φ(x2)|max≥
m,
由a=0,b=1,c=
,可得f(x)=2x2+1≥
(x+1)2在x∈[0,1]上恒成立,
∴
≥
(x+1)在x∈[0,1]上恒成立,
由(Ⅱ)知
≤(
-1)在x∈[0,1]上恒成立.
∴
(x+1)≤
≤(
-1)x+1在x∈[0,1]上恒成立.
又∵当x∈[0,1]时,1-x∈[0,1],
∴
(x+1)+
(1-x+1)≤φ(x)≤(
-1)x+1+(
-1)(1-x)+1,
即
≤φ(x)≤
+1,
∴|φ(x1)-φ(x2)|max=
+1-
≥
m,
则m≤1+
-
.
由f(x)=h(x),可得(c-2)x2+2cx+c-b=0,代入x=
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
由△=0,得c2=(c-2)(c-b) ②.
联立①②解得:b=1,c=
| 2 |
| 3 |
∴a=0,b=1,c=
| 2 |
| 3 |
(Ⅱ)f(x)=2x2+1,g(x)=(
| 3 |
当x=0时,由
| f(x) |
当m=1时,(
| 2x2+1 |
| 3 |
| 3 |
| 3 |
| 3 |
∴
| 2x2+1 |
| 3 |
∴对任意的x∈[-1,1],
| f(x) |
(Ⅲ)由题意可知,|φ(x1)-φ(x2)|max≥
| 3 |
由a=0,b=1,c=
| 2 |
| 3 |
| 2 |
| 3 |
∴
| 2x2+1 |
| ||
| 3 |
由(Ⅱ)知
| 2x2+1 |
| 3 |
∴
| ||
| 3 |
| f(x) |
| 3 |
又∵当x∈[0,1]时,1-x∈[0,1],
∴
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
即
| 6 |
| 3 |
∴|φ(x1)-φ(x2)|max=
| 3 |
| 6 |
| 3 |
则m≤1+
| ||
| 3 |
| 2 |
点评:本题考查了函数恒成立问题,考查了函数奇偶性性质的应用,训练了函数不等式恒成立条件的求法,体现了数学转化思想方法,关键是对题意的理解,综合考查了学生的逻辑思维能力抽象思维能力,是难度较大的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
若f(f(0))≥a2-1,则实数a的取值范围为( )
|
| A、[3,4] |
| B、[2,3] |
| C、[1,2] |
| D、[-1,2] |
若p是真命题,q是假命题,以下四个命题:p且q,p或q,非p,非q,其中假命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
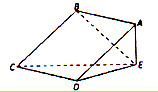 如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,
如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,