题目内容
已知数列{an}满足a1=-1,an+1=an+
,n∈N*,写出前5项,并写出这个数列的一个通项公式.
| 1 |
| n(n+1) |
考点:数列递推式
专题:计算题
分析:由递推公式依次求出数列的前5项,由归纳推理猜想出数列的一个通项公式,再由累加法、裂项相消法求出数列的通项公式.
解答:
解:因为a1=-1,an+1=an+
,n∈N*,
所以a2=a1+
=-
,a3=a2+
=-
,
同理可得,a4=-
,a,5=-
,
猜想得,an=-
,
由an+1=an+
得,an+1-an=
=
-
,
所以a2-a1=1-
,a3-a2=
-
,…,an-an-1=
-
,
以上n-1个式子相减得,an-a1=1-
,
又a1=-1,所以an=-
,
则这个数列的一个通项公式是an=-
.
| 1 |
| n(n+1) |
所以a2=a1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 3 |
同理可得,a4=-
| 1 |
| 4 |
| 1 |
| 5 |
猜想得,an=-
| 1 |
| n |
由an+1=an+
| 1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以a2-a1=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
以上n-1个式子相减得,an-a1=1-
| 1 |
| n |
又a1=-1,所以an=-
| 1 |
| n |
则这个数列的一个通项公式是an=-
| 1 |
| n |
点评:本题考查数列的递推公式,累加法、裂项相消法求出数列的通项公式,以及归纳推理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图是正方体的平面展开图,在这个正方体中,正确的命题是( )
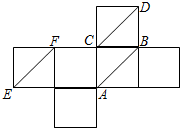

| A、BD与CF成60°角 |
| B、BD与EF成60°角 |
| C、AB与CD成60°角 |
| D、AB与EF成60°角 |