题目内容
若数列{an}的前n项和Sn=3n2+4n+1,讨论{an}是否为等差数列.
考点:等差关系的确定
专题:等差数列与等比数列
分析:利用数列{an}的前n项和Sn求出数列的通项公式,结合等差数列的定义进行判断即可.
解答:
解:当n≥2时,an=Sn-Sn-1=3n2+4n+1-[3(n-1)2+4(n-1)+1]=6n+1,
当n=1时,a1=S1=3+4+1=8,不满足上式.
故数列{an}的通项公式为an=
;
当n≥3时,an-an-1=(6n+1)-[6(n-1)+1]=6,
∵a2-a1=13-8=5≠6,
∴an-an-1不是一个与n无关的常数,
故数列{an}不是等差数列.
当n=1时,a1=S1=3+4+1=8,不满足上式.
故数列{an}的通项公式为an=
|
当n≥3时,an-an-1=(6n+1)-[6(n-1)+1]=6,
∵a2-a1=13-8=5≠6,
∴an-an-1不是一个与n无关的常数,
故数列{an}不是等差数列.
点评:本题考查了数列an与Sn的关系式,以及等差数列的定义,求出数列的通项公式是解决本题的关键..

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
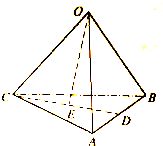 如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设
如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
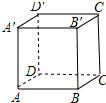 如图,正方体AC′的棱长为a.
如图,正方体AC′的棱长为a.