题目内容
7．函数$y=4x-\sqrt{2x-1}$的值域为[$\frac{15}{8}$，+∞）．分析 利用换元法，转化为一元二次函数进行求解即可．
解答 解：由2x-1≥0得x≥$\frac{1}{2}$，即函数的值域为[$\frac{1}{2}$，+∞），
设t=$\sqrt{2x-1}$，则t≥0，
且t2=2x-1，即x=$\frac{1+{t}^{2}}{2}$，
则原函数等价为y=4×$\frac{1+{t}^{2}}{2}$-t=2t2-t+2=2（t-$\frac{1}{4}$）2+$\frac{15}{8}$，
∵t≥0，∴y≥$\frac{15}{8}$，
即函数的值域为[$\frac{15}{8}$，+∞），
故答案为：[$\frac{15}{8}$，+∞）
点评 本题主要考查函数值域的求解，利用换元法，结合一元二次函数的性质是解决本题的关键．
练习册系列答案
相关题目
18．在区间（0，1）内任取两个数x，y，则满足y≥2x概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
2．
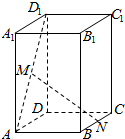如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2，AB=1，M为AD1的中点，N在BC上，且MN∥平面DCC1D1，则BN的长为（ ）
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2，AB=1，M为AD1的中点，N在BC上，且MN∥平面DCC1D1，则BN的长为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
12．等腰梯形ABCD，上底CD=1，腰AD=CB=$\sqrt{2}$，下底AB=3，以下底所在直线为x轴，则由斜二侧画法画出的直观图A′B′C′D′的面积为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | 2 |
19．不等式-x2+4x+5＜0的解集是（ ）
| A． | {x|x＞5或x＜-1} | B． | {x|x≥5或x≤-1} | C． | {x|-1＜x＜5} | D． | {x|-1≤x≤5} |