Question

2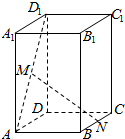．如图，在直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD为正方形，AA₁=2，AB=1，M为AD₁的中点，N在BC上，且MN∥平面DCC₁D₁，则BN的长为（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{3}$
• C． $\frac{1}{2}$
• D． $\frac{2}{3}$

Answer 1

分析 取AD的中点O，连接OM，ON，则OM∥DD₁，证明平面OMN∥平面DCC₁D₁，可得ON∥DC，即可求出BN的长．

解答 解：取AD的中点O，连接OM，ON，则OM∥DD₁，
∵OM?平面DCC₁D₁，DD₁?平面DCC₁D₁，
∴OM∥平面DCC₁D₁，
∵OM∩MN=M，
∴平面OMN∥平面DCC₁D₁，
∵平面ABCD∩平面OMN=ON，平面ABCD∩平面DCC₁D₁=DC，
∴ON∥DC，
∵O为AD的中点，
∴N为BC的中点，
∴BN=$\frac{1}{2}$．
故选：C．

点评 本题考查BN的长，考查线面、面面平行的判定，考查学生分析解决问题的能力，属于中档题．