Question

18．在区间（0，1）内任取两个数x，y，则满足y≥2x概率是（　　）

• A． $\frac{3}{4}$
• B． $\frac{1}{4}$
• C． $\frac{1}{2}$
• D． $\frac{2}{3}$

Answer 1

分析 该题涉及两个变量，故是与面积有关的几何概型，分别表示出满足条件的面积和整个区域的面积，最后利用概率公式解之即可．

解答 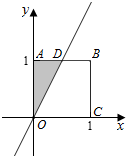解：在区间（0，1）上随机取两个数x，y，满足$\left\{\begin{array}{l}{0＜x＜1}\\{0＜y＜1}\end{array}\right.$，对应区域OABC的面积为1，
满足y≥2x，对应区域为△OAD如图，
其中D（$\frac{1}{2}$，1），则对应的面积的面积S=$\frac{1}{2}×1×\frac{1}{2}$=，$\frac{1}{4}$，
∴所求的概率为P=$\frac{\frac{1}{4}}{1}$=$\frac{1}{4}$．
故选：B

点评 本题主要考查了与面积有关的几何概率的求解，解题的关键是准确求出区域的面积，利用线性规划的知识进行求解是解决本题的关键．属于中档题