题目内容
16.在平面直角坐标系中,分别取与 x 轴,y 轴方向相同的两个单位向量作$\overrightarrow{i},\overrightarrow{j}$为基底,若向量,$\overrightarrow{a}=cos\frac{π}{3}\overrightarrow{i}+sin\frac{π}{3}\overrightarrow{j}$,$\overrightarrow{b}=cos\frac{2π}{3}\overrightarrow{i}+sin\frac{2π}{3}\overrightarrow{j}$,则|$\overrightarrow{a}-\overrightarrow{b}$|=1.分析 根据向量的加减运算和特殊角的三角函数值得到|$\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{i}$|,问题得以解决.
解答 解:∵$\overrightarrow{a}=cos\frac{π}{3}\overrightarrow{i}+sin\frac{π}{3}\overrightarrow{j}$,$\overrightarrow{b}=cos\frac{2π}{3}\overrightarrow{i}+sin\frac{2π}{3}\overrightarrow{j}$,
∴$\overrightarrow{a}-\overrightarrow{b}$=(cos$\frac{π}{3}$-cos$\frac{2π}{3}$)$\overrightarrow{i}$+(sin$\frac{π}{3}$-sin$\frac{2π}{3}$)$\overrightarrow{i}$=$\overrightarrow{i}$,
∴|$\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{i}$|=1,
故答案为:1.
点评 本题考查了特殊角的三角函数值,以及向量的加减运算,以及向量的模的计算,属于基础题.

练习册系列答案
相关题目
6.如果实数x、y满足关系$\left\{\begin{array}{l}{x+y-4≤0}\\{x-y≤0}\\{4x-y+4≥0}\end{array}\right.$,则(x-2)2+y2的最小值是( )
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
4.边长为1的正方形ABCD,将△ABC沿对角线AC折起,使△ABD为正三角形,则直线BD和平面ABC所成的角的大小为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
11.已知函数f(x)=ax-4+1(a>0,且a≠1)的图象经过定点A,而点A在幂函数g(x)=xα的图象上,则α=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
1.奇函数f(x)的定义域为R.若f(x+2)为偶函数,且f(1)=1,则f(5)+f(8)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
8.已知向量$\overrightarrow a$=(0,2,1),$\overrightarrow b$=(1,-1,2 )的夹角为( )
| A. | 0° | B. | 45° | C. | 90° | D. | 180° |
6.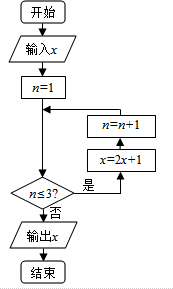 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |