题目内容
17.设Sn是数列{an}(n∈N*)的前n项和,a1=1,且Sn2=n2an+Sn-12,an≠0,n≥2,n∈N*.(1)证明:an+2-an=2(n∈N*);
(2)若an=log3bn,求数列{an•bn}的前n项和Tn.
分析 (1)由Sn2=n2an+Sn-12可得Sn+Sn-1=n2,从而可得an+1+an=2n+1,从而证明;
(2)由(1)可解得an=n,bn=3n,从而利用错位相减法求前n项和.
解答 解:(1)证明:∵Sn2=n2an+Sn-12,
∴n2an=(Sn+Sn-1)(Sn-Sn-1),
即n2an=(Sn+Sn-1)an,又∵an≠0,
故Sn+Sn-1=n2,
故Sn+1+Sn=(n+1)2,
故an+1+an=2n+1,
故an+2+an+1=2n+3,
故an+2-an=2(n∈N*);
(2)由题意可解得,a1=1,a2=2,
故an=n,
故log3bn=n,
故bn=3n,
故Tn=1•3+2•32+3•33+…+n•3n,
3Tn=1•32+2•33+3•34+…+n•3n+1,
故2Tn=n•3n+1-(3+32+33+…+3n)
=n•3n+1-$\frac{3({3}^{n}-1)}{3-1}$
=n•3n+1-$\frac{1}{2}$•3n+1+$\frac{3}{2}$,
故Tn=$\frac{(2n-1){3}^{n+1}+3}{4}$.
点评 本题考查了学生的化简运算能力及错位相减法求前n项和的应用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.已知向量$\overrightarrow a$=(0,2,1),$\overrightarrow b$=(1,-1,2 )的夹角为( )
| A. | 0° | B. | 45° | C. | 90° | D. | 180° |
6.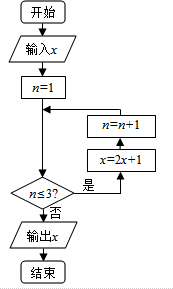 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |