题目内容
3.定义某种运算M=a?b,运算原理如图所示,则式子$(2tan\frac{π}{4})?sin\frac{π}{2}+(4cos\frac{π}{3})?{(\frac{1}{3})^{-1}}$的值为( )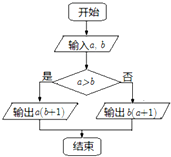
| A. | 4 | B. | 8 | C. | 11 | D. | 13 |
分析 模拟程序框图的运行过程,得出该程序框图运行的结果是计算并输出M=a?b=$\left\{\begin{array}{l}{a(b+1)}&{a>b}\\{b(a+1)}&{a≤b}\end{array}\right.$的值,利用特殊角的三角函数值计算比较,即可求值得解.
解答 解:模拟程序框图的运行过程,得出该程序框图运行的结果是计算并输出M=a?b=$\left\{\begin{array}{l}{a(b+1)}&{a>b}\\{b(a+1)}&{a≤b}\end{array}\right.$,
∵2tan$\frac{π}{4}$=2>sin$\frac{π}{2}$=1,4cos$\frac{π}{3}$=2<($\frac{1}{3}$)-1=3,
∴$(2tan\frac{π}{4})?sin\frac{π}{2}+(4cos\frac{π}{3})?{(\frac{1}{3})^{-1}}$
=2?1+2?3
=2×(1+1)+3×(2+1)=13.
故选:D.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,从而得出该程序框图运行的结果是什么,属于基础题.

练习册系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的斜率为2,且右焦点与抛物线y2=4$\sqrt{5}$x的焦点重合,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 2$\sqrt{5}$ |
14.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F1作倾斜角为$\frac{π}{6}$的直线交双曲线的右支交于点P,若|PF2|=|F1F2|,则双曲线的离心率是( )
| A. | $\sqrt{3}$-1 | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |
18.设平面区域D是由双曲线y2-$\frac{{x}^{2}}{4}$=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
15.已知全集U=R,A={-1},B={x|lg(x2-2)=lgx},则( )
| A. | A⊆B | B. | A∪B=∅ | C. | A?B | D. | (∁UA)∩B={2} |
13.已知函数f(x)=x2-$\frac{a}{x}$(a∈R),则下列结论正确的是( )
| A. | ?a∈R,f(x)是偶函数 | B. | ?a∈R,f(x)是奇函数 | ||
| C. | ?a∈(0,+∞),f(x)在(-∞,0)上是增函数 | D. | ?a∈(0,+∞),f(x)在(0,+∞)上是减函数 |