题目内容

15．已知全集U=R，A={-1}，B={x|lg（x2-2）=lgx}，则（　　）
A．A⊆BB．A∪B=∅C．A?BD．（∁UA）∩B={2}

分析 由lg（x2-2）=lgx，可得x2-2=x＞0，解得x，可得集合B．再利用集合的运算性质即可得出．

解答 解：由lg（x2-2）=lgx，可得x2-2=x＞0，解得x=2．∴B={2}．
∴（∁UA）∩B={x|x≠-1}∩{2}={2}．
故选：D．

点评 本题考查了集合的运算性质、方程的解法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
5．已知点F1，F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，点A是双曲线右支上一点，∠AF2F1=$\frac{2π}{3}$，且（$\overrightarrow{{F}_{2}{F}_{1}}$+$\overrightarrow{{F}_{2}A}$）•$\overrightarrow{{F}_{1}A}$=0，则此双曲线的离心率为（　　）
A．$\frac{1+\sqrt{5}}{2}$B．$\frac{1+\sqrt{3}}{2}$C．$\frac{3}{2}$D．$\frac{1+\sqrt{2}}{2}$
6．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线C2：$\frac{{y}^{2}}{{b}^{2}}$-$\frac{{x}^{2}}{{a}^{2}}$=1，其中b＞a＞0，则关于双曲线C1与C2的命题．
①渐近线相同；
②焦点相同；
③离心率e1，e2满足$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=1；
④两个双曲线焦点在同一圆上，
其中所有正确的命题序号为（　　）
A．①②③B．①③④C．②③④D．③④
3．定义某种运算M=a?b，运算原理如图所示，则式子$（2tan\frac{π}{4}）?sin\frac{π}{2}+（4cos\frac{π}{3}）?{（\frac{1}{3}）^{-1}}$的值为（　　）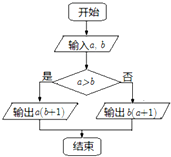
A．4B．8C．11D．13
10．设$a={log}_{\frac{2}{5}}2，b={（\frac{1}{2}）}^{\frac{1}{5}}，c={2}^{\frac{2}{5}}$，则a，b，c的大小关系是（　　）
A．c＞b＞aB．c＞a＞bC．a＞b＞cD．b＞c＞a
20．设方程|x2+3x-3|=a的解的个数为m，则m不可能等于（　　）
A．1B．2C．3D．4
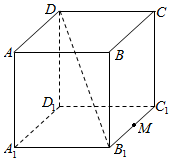7．如图AC1是棱长为2的正方体，M为B1C1的中点，给出下列命题：
①AB1与BC1成60°角；
②若$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{N{C}_{1}}$，面A1MN交CD于E，则CE=$\frac{1}{3}$；
③P点在正方形ABB1A1边界及内部运动，且MP⊥DB1，则P点轨迹长等于$\sqrt{2}$；
④E，F分别在DB1和A1C1上，且$\frac{DE}{E{B}_{1}}$=$\frac{{A}_{1}F}{F{C}_{1}}$=2，直线EF与AD1，A1D所成角分别是α，β，则α+β=$\frac{π}{2}$．
其中正确的命题有①③④．（写出所有正确命题的序号）
4．已知等差数列{an}，若a1=-11，a4+a6=-6，则an=2n-13．
5．函数$y=sinx（{-\frac{π}{3}＜x＜\frac{2π}{3}}）$的值域用区间表示为（-$\frac{\sqrt{3}}{2}$，1]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网