题目内容
8.设$α∈\{-2,-1,-\frac{1}{2},\frac{1}{3},\frac{1}{2},1,2,3\}$,则使幂函数f(x)=xα为偶函数,且在(0,+∞)是减函数的α值是-2.(写出所有符合条件的α值)分析 由幂函数y=xα为(0,+∞)上递减,得出α<0,又通过函数为偶函数,得出α为偶数,从而得出α的值.
解答 解:∵幂函数f(x)=xα为偶函数,∴α为偶数,
又f(x)在(0,+∞)是减函数,
∴α<0;
又∵α∈{-2,-1,-$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{2}$,1,2,3},
∴α=-2.
故答案为:-2.
点评 本题主要考查了幂函数单调性和奇偶性,要理解好幂函数单调性和奇偶性的定义并能灵活利用.

练习册系列答案
相关题目
16.从2015名学生中选50人组成参观团,先用简单随机抽样方法剔除15人,再将其余2000人从0到1999编号,按等距系统抽样方法选取,若第一组采用抽签法抽到的号码是30,则最后一组入选的号码是( )
| A. | 1990 | B. | 1991 | C. | 1989 | D. | 1988 |
3.定义某种运算M=a?b,运算原理如图所示,则式子$(2tan\frac{π}{4})?sin\frac{π}{2}+(4cos\frac{π}{3})?{(\frac{1}{3})^{-1}}$的值为( )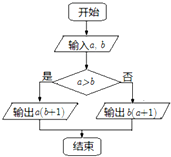

| A. | 4 | B. | 8 | C. | 11 | D. | 13 |
20.设方程|x2+3x-3|=a的解的个数为m,则m不可能等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |