题目内容

11．若函数f（x）=log${\;}_{\frac{1}{2}}$（x2-4x+3），则函数f（x）的单调递减区间是（3，+∞）．

分析 先求出函数的定义域，然后利用复合函数的单调性确定函数f（x）的单调递减区间．

解答 解：由x2-4x+3＞0，得x＜1或x＞3．
∴函数f（x）=log${\;}_{\frac{1}{2}}$（x2-4x+3）的定义域为（-∞，1）∪（3，+∞），
又内函数t=x2-4x+3在（3，+∞）上为增函数，
而外函数y=$lo{g}_{\frac{1}{2}}t$是定义域内的减函数，
∴复合函数f（x）的单调递减区间是（3，+∞）．
故答案为：（3，+∞）．

点评 本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．

练习册系列答案
相关题目
1．已知双曲线C：$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$的焦距为$10\sqrt{5}$，点P（1，2）在双曲线C的渐近线上，则双曲线C的方程为（　　）
A．$\frac{y^2}{20}-\frac{x^2}{5}=1$B．$\frac{y^2}{5}-\frac{x^2}{20}=1$C．$\frac{y^2}{100}-\frac{x^2}{25}=1$D．$\frac{y^2}{25}-\frac{x^2}{100}=1$
2．已知数列{an}是各项均不为0的等差数列，Sn为其前n项和，且满足an2=S2n-1（n∈N+）．若不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{{n+8•{{（-1）}^{n+1}}}}{n}$对任意的n∈N+恒成立，则实数λ的最大值为-15．
19．将由直线y=$\frac{2}{π}x$和曲线y=sinx，x∈[0，$\frac{π}{2}$]所围成的平面图形绕x轴旋转一周，求所得旋转体的体积．
6．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线C2：$\frac{{y}^{2}}{{b}^{2}}$-$\frac{{x}^{2}}{{a}^{2}}$=1，其中b＞a＞0，则关于双曲线C1与C2的命题．
①渐近线相同；
②焦点相同；
③离心率e1，e2满足$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=1；
④两个双曲线焦点在同一圆上，
其中所有正确的命题序号为（　　）
A．①②③B．①③④C．②③④D．③④
16．从2015名学生中选50人组成参观团，先用简单随机抽样方法剔除15人，再将其余2000人从0到1999编号，按等距系统抽样方法选取，若第一组采用抽签法抽到的号码是30，则最后一组入选的号码是（　　）
A．1990B．1991C．1989D．1988
3．定义某种运算M=a?b，运算原理如图所示，则式子$（2tan\frac{π}{4}）?sin\frac{π}{2}+（4cos\frac{π}{3}）?{（\frac{1}{3}）^{-1}}$的值为（　　）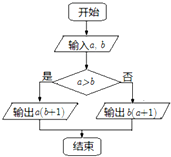
A．4B．8C．11D．13
20．设方程|x2+3x-3|=a的解的个数为m，则m不可能等于（　　）
A．1B．2C．3D．4
1．某人经营一个抽奖游戏，顾客花费2元可购买一次游戏机会，每次游戏中，顾客从装有1个人黑球，3个红球，6个白球的不透明袋子中依次不放回地摸出3个球（除颜色外其他都相同），根据摸出的球的颜色情况进行兑奖，顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金a元、10元、5元、1元．若经营者将顾客摸出的3个球的颜色情况分成以下类别：A：1个黑球2个红球；B：3个红球；C：恰有1个白球；D：恰有2个白球；E：3个白球．且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次．
（1）请写出一至四等奖分别对应的类别（写出字母即可）；
（2）若经营者不打算在这个游戏的经营中亏本，求a的最大值；
（3）若a=50，当顾客摸出的第一个球是红球时，求他领取的奖金的平均值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网