题目内容
18．设平面区域D是由双曲线y2-$\frac{{x}^{2}}{4}$=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形（含边界与内部）．若点（x，y）∈D，则x+y的最小值为（ ）| A． | -1 | B． | 1 | C． | 0 | D． | 3 |
分析 先求出抛物线的准线方程和双曲线的渐近线方程，画出三角形平面区域，根据z=x+y的最小值为斜率为-1的直线的纵截距的最小值，即可求出z=x+y的最小值．
解答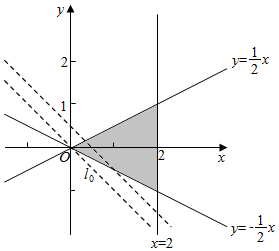 
解：抛物线y2=-8x的准线方程为x=2，
双曲线y2-$\frac{{x}^{2}}{4}$=1的两条渐近线方程为y=±$\frac{1}{2}$x，
由题意，三角形平面区域的边界为x=2，y=±$\frac{1}{2}$x，
设z=x+y即y=z-x，
则z=z-x的最小值为斜率为-1的直线的纵截距的最小值．
作出直线l0：y=-x，平移可得，
当直线l0过原点时，取得最小值0．
故选：C．
点评 本题以双曲线、抛物线为载体，考查线性规划知识，考查函数的最值的求解，正确理解目标函数的几何意义是解题的关键．
练习册系列答案
相关题目
8．已知双曲线的左、右焦点分别是F1、F2，过F2的直线交双曲线的右支于P、Q两点，若|PF1|=|F1F2|，且3|PF2|=2|QF2|，则该双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{10}{3}$ | C． | 2 | D． | $\frac{7}{5}$ |
9．双曲线2x2-y2=1的渐近线方程是（ ）
| A． | y=±$\frac{1}{2}$x | B． | y=±2x | C． | y=±$\frac{\sqrt{2}}{2}$x | D． | y=±$\sqrt{2}$x |
3．定义某种运算M=a?b，运算原理如图所示，则式子$（2tan\frac{π}{4}）?sin\frac{π}{2}+（4cos\frac{π}{3}）?{（\frac{1}{3}）^{-1}}$的值为（ ）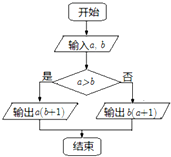
| A． | 4 | B． | 8 | C． | 11 | D． | 13 |
10．设$a={log}_{\frac{2}{5}}2，b={（\frac{1}{2}）}^{\frac{1}{5}}，c={2}^{\frac{2}{5}}$，则a，b，c的大小关系是（ ）
| A． | c＞b＞a | B． | c＞a＞b | C． | a＞b＞c | D． | b＞c＞a |
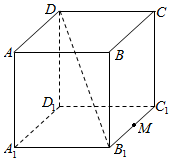如图AC1是棱长为2的正方体，M为B1C1的中点，给出下列命题：