题目内容
已知椭圆方程为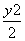 +x2=1,斜率为k(k≠0)的直线l过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
+x2=1,斜率为k(k≠0)的直线l过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
(1)求m的取值范围;
(2)求△MPQ面积的最大值.
解:(1)设直线l的方程为y=kx+1,
由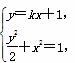
可得(k2+2)x2+2kx-1=0.
设P(x1,y1),Q(x2,y2),则x1+x2=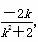 ,x1x2=-
,x1x2=-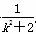 .可得y1+y2=k(x1+x2)+2=
.可得y1+y2=k(x1+x2)+2=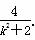 .
.
设线段PQ的中点为N,则点N的坐标为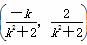 ,
,
由题意有kMN·k=-1,可得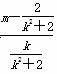 ·k=-1,可得m=
·k=-1,可得m=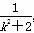 ,又k≠0,所以0<m<
,又k≠0,所以0<m<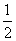 .
.
(2)设椭圆的焦点为F,
则S△MPQ=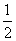 ·|FM|·|x1-x2|=
·|FM|·|x1-x2|=
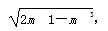 ,
,
所以△MPQ的面积为
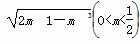 设f(m)=m(1-m)3,
设f(m)=m(1-m)3,
则f′(m)=(1-m)2(1-4m).
可知f(m)在区间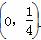 上递增,在区间
上递增,在区间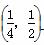 上递减.
上递减.
所以,当m=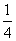 时,
时,
f(m)有最大值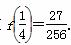
即当m=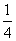 时,△MPQ的面积有最大值
时,△MPQ的面积有最大值 .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
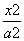 +
+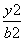 =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=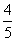 ,则C的离心率e=________.
,则C的离心率e=________.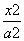 -
-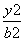 =1(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是
=1(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是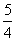 ,且
,且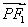 ·
·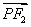 ,=0,若△PF1F2的面积为9,则a+b的值为( )
,=0,若△PF1F2的面积为9,则a+b的值为( ) -
- =-1(a>0,b>0)与抛物线y=
=-1(a>0,b>0)与抛物线y= x2有一个公共焦点F,双曲线上过点F且垂直实轴的弦长为
x2有一个公共焦点F,双曲线上过点F且垂直实轴的弦长为 ,则双曲线的离心率等于________.
,则双曲线的离心率等于________. 和
和 是空间中两个不同的平面,下列叙述中,正确的是 。(填序号)
是空间中两个不同的平面,下列叙述中,正确的是 。(填序号) ,
, ,所以
,所以 ;
; ,所以
,所以 ;
; ,
, ,
, ,所以
,所以 ,所以
,所以 。
。 在区间[0,2]上的最大值比最小值大
在区间[0,2]上的最大值比最小值大 ,则
,则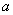 的值为( )
的值为( ) B.
B. C.
C. D.
D.