题目内容
某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下:(单位:cm)
(Ⅰ)根据抽测结果,画出茎叶图,并根据你画的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论;
(Ⅱ)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率.
| 南方158 | 170 | 166 | 169 | 180 | 175 | 171 | 176 | 162 | 163 |
| 北方183 | 173 | 169 | 163 | 179 | 171 | 157 | 175 | 178 | 166 |
(Ⅱ)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率.
考点:茎叶图,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)根据抽测结果,画出茎叶图如右图,利用茎叶图作出统计结论.
(2)南方大学生身高不低于170的有170,180,175,171,176,从中抽取3个相当于从中抽取3个,共有
=10种抽法,低于175的只有
=3个,由此能求出结果.
(2)南方大学生身高不低于170的有170,180,175,171,176,从中抽取3个相当于从中抽取3个,共有
| C | 3 5 |
| C | 2 3 |
解答:
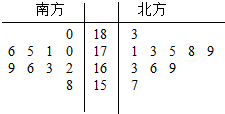 解:(1)根据抽测结果,画出茎叶图如右图所示:
解:(1)根据抽测结果,画出茎叶图如右图所示:
统计结论:
①北方大学生的平均身高大于南方大学生的平均身高;
②南方大学生的身高比北方大学的身高更整齐;
③南方大学生的身高的中位数为169.5cm,
北方大学生的身高的中位数为172cm.
(2)南方大学生身高不低于170的有170,180,175,171,176,
从中抽取3个相当于从中抽取3个,共有
=10种抽法,
低于175的只有
=3个,
所以共有3种,概率为p=
.
 解:(1)根据抽测结果,画出茎叶图如右图所示:
解:(1)根据抽测结果,画出茎叶图如右图所示:统计结论:
①北方大学生的平均身高大于南方大学生的平均身高;
②南方大学生的身高比北方大学的身高更整齐;
③南方大学生的身高的中位数为169.5cm,
北方大学生的身高的中位数为172cm.
(2)南方大学生身高不低于170的有170,180,175,171,176,
从中抽取3个相当于从中抽取3个,共有
| C | 3 5 |
低于175的只有
| C | 2 3 |
所以共有3种,概率为p=
| 3 |
| 10 |
点评:本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意茎叶图的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知F1、F2是椭圆的两个焦点,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则该椭圆的离心率为( )
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
已知m,n是两条不同直线,α,β是两个不同的平面,且m∥α,n?β,则下列叙述正确的是( )
| A、若α∥β,则m∥n |
| B、若m∥n,则α∥β |
| C、若n⊥α,则m⊥β |
| D、若m⊥β,则α⊥β |
幂函数f(x)的图象在点A(1,f(1))处的切线斜率为3,且关于x的不等式f(x)>ax2+x在(2,4)上恒成立,则实数a的取值范围为 ( )
A、[
| ||
B、(
| ||
C、(-∞,
| ||
D、(-∞,
|