题目内容
下列对应中,是集合A到集合B的映射的个数为( )
①A={1,3,5,7,9},B={2,4,6,8,10},对应法则f:x→y=x+1,x∈A,y∈B;
②A={x|x是三角形},B={x|x圆},对应法则f:每一个三角形都对应它的内切圆;
③A={x|x∈R},B{y|y≥0}.对应法则f:x→y=x2,x∈A,y∈B.
①A={1,3,5,7,9},B={2,4,6,8,10},对应法则f:x→y=x+1,x∈A,y∈B;
②A={x|x是三角形},B={x|x圆},对应法则f:每一个三角形都对应它的内切圆;
③A={x|x∈R},B{y|y≥0}.对应法则f:x→y=x2,x∈A,y∈B.
| A、0 | B、1 | C、2 | D、3 |
考点:映射
专题:计算题,函数的性质及应用
分析:由题意,根据映射的定义对三个对应依次判断即可.
解答:
解:①A={1,3,5,7,9},B={2,4,6,8,10},对应法则f:x→y=x+1,x∈A,y∈B;是映射;
②每一个三角形都有且只有一个内切圆,故A={x|x是三角形},B={x|x是圆},对应法则f:每一个三角形都对应它的内切圆是映射;
③A={x|x∈R},B{y|y≥0}.对应法则f:x→y=x2,x∈A,y∈B;是映射.
故选D.
②每一个三角形都有且只有一个内切圆,故A={x|x是三角形},B={x|x是圆},对应法则f:每一个三角形都对应它的内切圆是映射;
③A={x|x∈R},B{y|y≥0}.对应法则f:x→y=x2,x∈A,y∈B;是映射.
故选D.
点评:本题考查了映射的概念,属于基础题.

练习册系列答案
相关题目
数列-1,4,-7,10,-13,…的通项公式an为( )
| A、2n-1 |
| B、-3n+2 |
| C、(-1)n3n-2 |
| D、(-1)n(3n-2) |
“a=4”是“函数f(x)=x2+ax+1在区间[-2,+∞)上为增函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口的直径为60cm,灯深40cm,则抛物线的标准方程可能是( )
A、x2=-
| ||
B、y2=
| ||
C、y2=
| ||
D、x2=-
|
下列命题中正确的是( )
A、y=x+
| ||||
B、y=
| ||||
C、y=sin2x+
| ||||
D、y=2-3x-
|
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.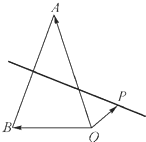 如图,P为△AOB所在平面内一点,向量
如图,P为△AOB所在平面内一点,向量