题目内容
曲线y=sinx与直线x=0、x=
、x轴所围成的图形的面积为 .
| 2π |
| 3 |
考点:定积分在求面积中的应用
专题:导数的概念及应用
分析:先做出函数y=sinx的图象,然后确定出交点,积分区间,则问题可解.
解答:
解:由题意,所求的面积为图中阴影部分:
故S=
sinxdx=-cosx
=-cos
+cos0=
.
故答案为
.

故S=
| ∫ |
0 |
| | |
0 |
| 2π |
| 3 |
| 3 |
| 2 |
故答案为
| 3 |
| 2 |

点评:本题考查了定积分的几何意义及其求法,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
设 f(x)=|lnx|,若函数 g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
“a=4”是“函数f(x)=x2+ax+1在区间[-2,+∞)上为增函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
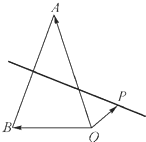 如图,P为△AOB所在平面内一点,向量
如图,P为△AOB所在平面内一点,向量