题目内容
设a是一个自然数,f(a)是a的各位数字的平方和,定义数列{an}:a1是自然数,an=f(an-1)(n∈N*,n≥2).
(Ⅰ)求f(99),f(2014);
(Ⅱ)若a1≥100,求证:a1>a2;
(Ⅲ)当a1<1000时,求证:存在m∈N*,使得a3m=a2m.
(Ⅰ)求f(99),f(2014);
(Ⅱ)若a1≥100,求证:a1>a2;
(Ⅲ)当a1<1000时,求证:存在m∈N*,使得a3m=a2m.
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)利用新定义,可求f(99),f(2014);
(Ⅱ)假设a1是一个n位数(n≥3),设出a1,由a2=f(a1)可得,a2=bn2+bn-12+…+b32+b22+b12,作差,即可得证;
(Ⅲ)利用数学归纳法进行证明即可.
(Ⅱ)假设a1是一个n位数(n≥3),设出a1,由a2=f(a1)可得,a2=bn2+bn-12+…+b32+b22+b12,作差,即可得证;
(Ⅲ)利用数学归纳法进行证明即可.
解答:
(Ⅰ)解:f(99)=92+92=162;f(2014)=22+02+12+42=21. …(5分)
(Ⅱ)证明:假设a1是一个n位数(n≥3),
那么可以设a1=bn•10n-1+bn-1•10n-2+…+b3•102+b2•10+b1,
其中0≤bi≤9且bi∈N(1≤i≤n),且bn≠0.
由a2=f(a1)可得,a2=bn2+bn-12+…+b32+b22+b12.a1-a2=(10n-1-bn)bn+(10n-2-bn-1)bn-1+…+(102-b3)b3+(10-b2)b1+(1-b1)b1,所以a1-a2≥(10n-1-bn)bn-(b1-1)b1.
因为bn≠0,所以(10n-1-bn)bn≥99.
而(b1-1)b1≤72,
所以a1-a2>0,即a1>a2. …(9分)
(Ⅲ)证明:由a1<1000,即a1≤999,可知a2≤92+92+92=243.
同理an≤999,可知an+1≤92+92+92=243.
由数学归纳法知,对任意n∈N*,有an≤999.
即对任意n∈N*,有an∈{1,2,3,…,999}.
因此,存在p,q∈N*(p<q),有ap=aq.
则ap+1=aq+1,ap+2=aq+2,…,aq-1=aq+q-p-1,
可得对任意n∈N*,n≥p,有an+q-p=an.
设q-p=T,即对任意n≥p,有an+T=an.
若T≥p,取m=T,n=2m,则有a3m=a2m.
若T<p,由an+T=an,可得an+pT=an,
取m=pT,n=2m,则有a3m=a2m. …(14分)
(Ⅱ)证明:假设a1是一个n位数(n≥3),
那么可以设a1=bn•10n-1+bn-1•10n-2+…+b3•102+b2•10+b1,
其中0≤bi≤9且bi∈N(1≤i≤n),且bn≠0.
由a2=f(a1)可得,a2=bn2+bn-12+…+b32+b22+b12.a1-a2=(10n-1-bn)bn+(10n-2-bn-1)bn-1+…+(102-b3)b3+(10-b2)b1+(1-b1)b1,所以a1-a2≥(10n-1-bn)bn-(b1-1)b1.
因为bn≠0,所以(10n-1-bn)bn≥99.
而(b1-1)b1≤72,
所以a1-a2>0,即a1>a2. …(9分)
(Ⅲ)证明:由a1<1000,即a1≤999,可知a2≤92+92+92=243.
同理an≤999,可知an+1≤92+92+92=243.
由数学归纳法知,对任意n∈N*,有an≤999.
即对任意n∈N*,有an∈{1,2,3,…,999}.
因此,存在p,q∈N*(p<q),有ap=aq.
则ap+1=aq+1,ap+2=aq+2,…,aq-1=aq+q-p-1,
可得对任意n∈N*,n≥p,有an+q-p=an.
设q-p=T,即对任意n≥p,有an+T=an.
若T≥p,取m=T,n=2m,则有a3m=a2m.
若T<p,由an+T=an,可得an+pT=an,
取m=pT,n=2m,则有a3m=a2m. …(14分)
点评:本题考查数列的应用,考查新定义,考查数学归纳法,考查学生分析解决问题的能力,难度较大.

练习册系列答案
相关题目
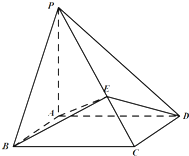 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=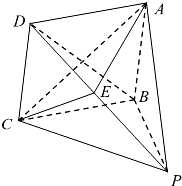 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.