题目内容
设函数f（x）=sin（ωx+φ）+
cos（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，且满足f（-x）=f（x），则函数f（x）的单调增区间为 ．
| 3 |
| π |
| 2 |
考点：两角和与差的正弦函数,正弦函数的图象
专题：三角函数的图像与性质
分析：化简函数解析式可得f（x）=2sin（ωx+φ+
），由最小正周期为π，可求ω，由f（-x）=f（x），且|φ|＜
，可解得φ，由2kπ-
≤2x≤2kπ+
，k∈Z，可解得函数f（x）的单调增区间．
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答：
解：∵f（x）=sin（ωx+φ）+
cos（ωx+φ）=2sin[（ωx+φ）+
]=2sin（ωx+φ+
），最小正周期为π，
∴ω=
=2，
∵f（-x）=f（x），
∴可得：φ+
=kπ，k∈Z，
∵|φ|＜
，
∴解得：φ=-
，
∴f（x）=2sin2x，
∴由2kπ-
≤2x≤2kπ+
，k∈Z，可解得：kπ-
≤x≤kπ+
，k∈Z
故答案为：[kπ-
，kπ+
]，k∈Z
| 3 |
| π |
| 3 |
| π |
| 3 |
∴ω=
| 2π |
| π |
∵f（-x）=f（x），
∴可得：φ+
| π |
| 3 |
∵|φ|＜
| π |
| 2 |
∴解得：φ=-
| π |
| 3 |
∴f（x）=2sin2x，
∴由2kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
故答案为：[kπ-
| π |
| 4 |
| π |
| 4 |
点评：本题主要考查了两角和与差的正弦函数公式的应用，正弦函数的图象和性质，考查了三角函数周期公式的应用，属于基本知识的考查．
练习册系列答案
相关题目
函数y=lg（x2-2x+a）的值域不可能是（ ）
| A、（-∞，0] | B、[0，+∞） |
| C、[1，+∞） | D、R |
已知a、b、c为集合A={1，2，3，4，5}中三个不同的数，通过如图所示算法框图给出的一个算法输出一个整数a，则输出的数a=5的概率是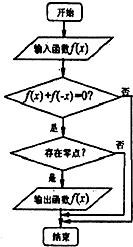
某程序框图如图所示，现依次输入如下四个函数：