题目内容
【题目】如图有一景区的平面图是一半圆形,其中直径长为![]() 两点在半圆弧上满足
两点在半圆弧上满足![]() ,设
,设![]() ,现要在景区内铺设一条观光通道,由
,现要在景区内铺设一条观光通道,由![]() 和
和 ![]() 组成.
组成.
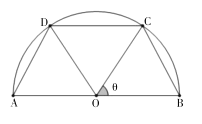
(1)用![]() 表示观光通道的长
表示观光通道的长![]() ,并求观光通道
,并求观光通道![]() 的最大值;
的最大值;
(2)现要在景区内绿化,其中在![]() 中种植鲜花,在
中种植鲜花,在![]() 中种植果树,在扇形
中种植果树,在扇形![]() 内种植草坪,已知单位面积内种植鲜花和种植果树的利润均是种植草坪利润的
内种植草坪,已知单位面积内种植鲜花和种植果树的利润均是种植草坪利润的![]() 倍,则当
倍,则当![]() 为何值时总利润最大?
为何值时总利润最大?
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,总利润取最大值.
时,总利润取最大值.
【解析】
(1)根据直径的长度和角度![]() 计算出
计算出![]() 的长度,写出
的长度,写出![]() 的函数解析式,注意定义域,判断
的函数解析式,注意定义域,判断![]() 取何值的时候
取何值的时候![]() 有最大值并计算出最大值;
有最大值并计算出最大值;
(2)设出单位面积的利润,将三个三角形的面积计算出来并求利润和的表示,利用导数去计算函数的最值,确定取等号时![]() 的取值.
的取值.
(1)作![]() ,垂足为
,垂足为![]() ,在直角三角形
,在直角三角形![]() 中,
中,![]() ,
,
所以![]() ,
,
同理作![]() ,垂足为
,垂足为![]() ,
,![]() ,所以
,所以![]() ,如图:
,如图:

所以 ,
,
当![]() 时,取最大值
时,取最大值![]() .
.
(2)设种植草坪单位面积的利润为![]() ,
,
![]() ,
,
则总利润![]() ,
,
![]()
![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]()
![]() ,所以
,所以![]() 在
在![]() 递增,
递增,![]() 递减,
递减,
所以当![]() 时总利润取最大值,最大值为
时总利润取最大值,最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目