题目内容
【题目】在正方体![]() 中,点E,F分别是棱
中,点E,F分别是棱![]() 上的动点,且
上的动点,且![]() .当三棱锥
.当三棱锥![]() 的体积取得最大值时,记二面角
的体积取得最大值时,记二面角![]() 、
、![]() 、
、![]() 平面角分别为
平面角分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意,设正方体的棱长为2,当三棱锥![]() 的体积取得最大值时,即底面积
的体积取得最大值时,即底面积![]() 最大时,推得点E,F在棱
最大时,推得点E,F在棱![]() 上的位置,以
上的位置,以![]() 为原点,
为原点,![]() 为x轴,
为x轴,![]() 为y轴,
为y轴,![]() 为z轴建立坐标系,利用向量法计算出
为z轴建立坐标系,利用向量法计算出![]() ,
,![]() ,
,![]() 的余弦值,即可得出答案。
的余弦值,即可得出答案。
如图所示,设正方体的棱长为![]() ,线段
,线段![]() 的长为x,, 底面积
的长为x,, 底面积![]() ,当三棱锥
,当三棱锥![]() 的体积取得最大值时,即底面积
的体积取得最大值时,即底面积![]() 最大时,此时
最大时,此时![]() 。
。
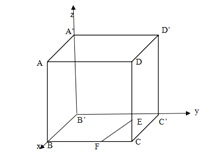
以![]() 为原点,
为原点,![]() 为x轴,
为x轴,![]() 为y轴,
为y轴,![]() 为z轴建立坐标系,则
为z轴建立坐标系,则![]() ,可得
,可得![]()
设面![]() 的法向量为
的法向量为![]() ,面
,面![]() 的法向量为
的法向量为![]() ,面
,面![]() 的法向量为
的法向量为![]() ,面
,面![]() 的法向量为
的法向量为![]() ,则
,则
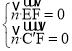

可得,![]() ,
,![]() ,
,![]() ,
,![]()
由图可知,![]() ,
,![]() ,
,![]() 均为锐角,则
均为锐角,则
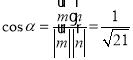 ,同理可得
,同理可得![]() ,
,![]()
得![]() ,所以
,所以![]() ,故答案选:A。
,故答案选:A。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.
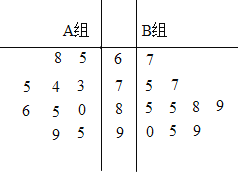
(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: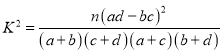 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|