题目内容
证明：f（x）=x+
在（3，+∞）上是增函数，在（2，3]上是减函数．
| 1 |
| x-2 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用函数单调性的定义证明．
解答：
证明：设任意的x1，x2∈（3，+∞），且x1＜x2，则
f（x1）-f（x2）=(x1+
)-(x2-
)=（x1-x2）•
∵x1，x2∈（3，+∞），且x1＜x2，
∴x1-x2＜0，x1-2＞1，x2-2＞1，（x1-2）（x2-2）＞1，
∴（x1-x2）•
＜0，∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴f（x）=x+
在（3，+∞）上是增函数．
同理可证，f（x）=x+
在（2，3]上是减函数．
f（x1）-f（x2）=(x1+
| 1 |
| x1-2 |
| 1 |
| x2+2 |
| (x1-2)(x2-2)-1 |
| (x1-2)(x2-2) |
∵x1，x2∈（3，+∞），且x1＜x2，
∴x1-x2＜0，x1-2＞1，x2-2＞1，（x1-2）（x2-2）＞1，
∴（x1-x2）•
| (x1-2)(x2-2)-1 |
| (x1-2)(x2-2) |
∴f（x）=x+
| 1 |
| x-2 |
同理可证，f（x）=x+
| 1 |
| x-2 |
点评：本题主要考查学生运用定义证明函数单调性的能力，属基础题．
练习册系列答案
相关题目
已知命题P：复数z=
在复平面内所对应的点位于第四象限；命题q：?x＞0，x=cosx，则下列命题中为真命题的是（ ）
| 1+i |
| i |
| A、（￢p）∧（￢q） |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、p∧q |
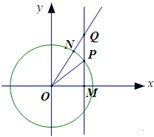在直角坐标系xOy中，点p是单位圆上位于第一象限的动点，过p作x轴的垂线与射线y=xtanθ（x≥0，0＜θ＜