题目内容
已知等差数列{an},的前n项和为Sn,且a2=2,S5=15,数列{bn}满足b1=
,bn+1=
bn.
(1)求数列{an},{bn}的通项公式;
(2)记Tn为数列{bn}的前n项和,f(n)=
,试问f(n)是否存在最大值,若存在,求出最大值,若不存在请说明理由.
| 1 |
| 2 |
| n+1 |
| 2n |
(1)求数列{an},{bn}的通项公式;
(2)记Tn为数列{bn}的前n项和,f(n)=
| 2Sn(2-Tn) |
| n+2 |
考点:数列的求和,数列递推式
专题:计算题,等差数列与等比数列
分析:(1)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an,
将bn+1=
bn整理,得到{
}是首项为
,公比为
的等比数列,应用等比数列的通项即可求出bn;
(2)运用错位相减法求出前n项和Tn,化简f(n),运用相邻两项的差f(n+1)-f(n),判断f(n)的增减性,从而判断f(n)是否存在最大值.
将bn+1=
| n+1 |
| 2n |
| bn |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
(2)运用错位相减法求出前n项和Tn,化简f(n),运用相邻两项的差f(n+1)-f(n),判断f(n)的增减性,从而判断f(n)是否存在最大值.
解答:
解:(1)设等差数列{an}首项为a1,公差为d,
则
解得a1=1,d=1,
∴an=n,
又
=
,
即{
}是首项为
,公比为
的等比数列,
∴
=
(
)n-1,
∴bn=
;
(2)由(1)得:Tn=
+
+
+…+
,
Tn=
+
+
+…+
+
,
相减,得
Tn=
+
+
+…+
-
=
-
,
∴Tn=2-
,又Sn=
n(n+1),
∴f(n)=
=
,
∴f(n+1)-f(n)=
-
=
,
当n>3时,f(n+1)-f(n)<0,数列{f(n)}是递减数列,
又f(1)=1,f(2)=
,f(3)=
∴f(n)存在最大值,且为
.
则
|
∴an=n,
又
| bn+1 |
| n+1 |
| bn |
| 2n |
即{
| bn |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| bn |
| n |
| b1 |
| 1 |
| 1 |
| 2 |
∴bn=
| n |
| 2n |
(2)由(1)得:Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n-1 |
| 2n |
| n |
| 2n+1 |
相减,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| ||||
1-
|
| n |
| 2n+1 |
∴Tn=2-
| n+2 |
| 2n |
| 1 |
| 2 |
∴f(n)=
| 2Sn(2-Tn) |
| n+2 |
| n2+n |
| 2n |
∴f(n+1)-f(n)=
| (n+1)2+n+1 |
| 2n+1 |
| n2+n |
| 2n |
| (n+1)(2-n) |
| 2n+1 |
当n>3时,f(n+1)-f(n)<0,数列{f(n)}是递减数列,
又f(1)=1,f(2)=
| 3 |
| 2 |
| 3 |
| 2 |
∴f(n)存在最大值,且为
| 3 |
| 2 |
点评:本题主要考查等差数列和等比数列的通项和前n项和的运用,考查数列的求和方法:错位相减法,以及应用相邻两项的差来判断数列的增减,应掌握,同时考查基本的运算能力.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
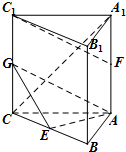 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.