题目内容

已知
sinα-cosα
sinα+cosα
=3，则tan2α等于
 
．
考点：二倍角的正切,同角三角函数基本关系的运用
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系求出tanα，再利用二倍角公式求得tan2α的值．
解答： 解：∵已知
sinα-cosα
sinα+cosα
=
tanα-1
tanα+1
=3，解得tanα=-2，
∴tan2α=
2tanα
1-tan2α
=
4
3
，
故答案为：
4
3
．
点评：本题主要考查同角三角函数的基本关系，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
盒子装中有形状、大小完全相同的五张卡片，分别标有数字1，2，3，4，5．现每次从中任意抽取一张，取出后不再放回．
（1）若抽取三次，求前两张卡片所标数字之和为偶数的条件下，第三张为奇数的概率；
（2）若不断抽取，直至取出标有偶数的卡片为止，设抽取次数为ξ，求随机变量ξ的分布列及数学期望．
证明：f（x）=x+
1
x-2
在（3，+∞）上是增函数，在（2，3]上是减函数．
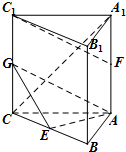如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB⊥AC，AC=AB=AA1，E、F分别是棱BC，A1A的中点，G为棱CC1上的一点，且C1F∥平面AEG．
（Ⅰ）求
CG
CC1
的值；
（Ⅱ）求证：EG⊥A1C；
（Ⅲ）求二面角A1-AG-E的余弦值．
（1+x）（1-x）3展开式中x3的系数是
 
．
执行如图所示算法的伪代码，则输出S的值为
 
．
函数f（x）=-x3+3x2在[-1，1]上的最大、小值分别为M和m，则
∫
M
m
f（x）dx=
 
．
对于集合A，如果定义了一种运算“⊕”，使得集合A中的元素间满足下列4个条件：
（ⅰ）?a，b∈A，都有a⊕b∈A；
（ⅱ）?e∈A，使得对?a∈A，都有e⊕a=a⊕e=a；
（ⅲ）?a∈A，?a′∈A，使得a⊕a′=a′⊕a=e；
（ⅳ）?a，b，c∈A，都有（a⊕b）⊕c=a⊕（b⊕c），
则称集合A对于运算“⊕”构成“对称集”．
下面给出三个集合及相应的运算“⊕”：
①A={整数}，运算“⊕”为普通加法；
②A={复数}，运算“⊕”为普通减法；
③A={正实数}，运算“⊕”为普通乘法．
其中可以构成“对称集”的有
 
．（把所有正确的序号都填上）
设函数f（x）的定义域为D，如果?x∈D，?y∈D，使得f（x）=-f（y）成立，则称函数f（x）为“Ω函数”．给出下列四个函数：
①y=sinx；
②y=2x；
③y=
1
x-1
；
④f（x）=lnx，
则其中“Ω函数”共有（　　）
A、1个B、2个C、3个D、4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网