��Ŀ����
��֪��ԲC��
+
=1��a��b��0������ΪF�����Ҷ���ֱ�ΪA��B������F����б��Ϊ
��ֱ��l����Բ��C��D���㣬��ԲC��������Ϊ
��
•
-
•
=-
��
��1������ԲC�ķ��̣�
��2����P1��P2����Բ�ϲ�ͬ���㣬P1��P2��x�ᣬԲR����P1��P2������Բ������һ�㶼����ԲR�ڣ����ԲRΪ����Բ������Բ������ԲC�Ƿ���ڹ���F������Բ�������ڣ������R�����ꣻ�������ڣ�˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
| �� |
| 4 |
| ||
| 2 |
| AC |
| AD |
| BC |
| BD |
32
| ||
| 5 |
��1������ԲC�ķ��̣�
��2����P1��P2����Բ�ϲ�ͬ���㣬P1��P2��x�ᣬԲR����P1��P2������Բ������һ�㶼����ԲR�ڣ����ԲRΪ����Բ������Բ������ԲC�Ƿ���ڹ���F������Բ�������ڣ������R�����ꣻ�������ڣ�˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1����������Ϊ
����a=2b��c=
b��ֱ��l�ķ���Ϊy=x+
b���ɷ�����
����5x2+8
bx+8b2=0���ɴ�������֪�����������Բ���̣�
��2������Բ�ĶԳ��ԣ���P1��m��n����P2��m��-n������R��x���ϣ����R��t��0����ԲR�ķ���Ϊ����x-t��2+y2=��m-t��2+n2���ɴ���������Բ��������֪�����������ԲC���ڷ�������������Բ����R�������ǣ�-
��0����
| ||
| 2 |
| 3 |
| 3 |
|
| 3 |
��2������Բ�ĶԳ��ԣ���P1��m��n����P2��m��-n������R��x���ϣ����R��t��0����ԲR�ķ���Ϊ����x-t��2+y2=��m-t��2+n2���ɴ���������Բ��������֪�����������ԲC���ڷ�������������Բ����R�������ǣ�-
| ||
| 2 |
���
�⣺��1����Ϊ������Ϊ
������a=2b��c=
b��
������Բ���̿ɻ�Ϊ��
+
=1��
ֱ��l�ķ���Ϊy=x+
b������2�֣�
�ɷ�����
���ã�x2+4(x+
b)2=4b2��
��5x2+8
bx+8b2=0������4�֣�
��C��x1��y1����D��x2��y2������x1+x2=-
b������5�֣�
��
•
-
•
=��x1+a��y1��•��x2+a��y2��-��x1-a��y1��•��x2-a��y2��=2a��x1+x2����
��4b•��-
b��=-
�����b=1��
����Բ������
+y2=1������7�֣�
��2������Բ�ĶԳ��ԣ�������P1��m��n����P2��m��-n����
��R��x���ϣ����R��t��0����
��ԲR�ķ���Ϊ����x-t��2+y2=��m-t��2+n2��
������Բ����֪������Բ�ϵĵ㵽��R�������Сֵ��|P1R|��
���M��x��y������ԲC������һ�㣬
��|MR|2=��x-t��2+y2=
x2-2tx+t2+1������9�֣�
��x=mʱ��|MR|2��С����m=-
=
���١���10�֣�
��ԲR����F�����ԣ�-
-t��2=��m-t��2+n2���ڡ���11�֣�
��P1����Բ�ϣ���n2=1-
���ۡ���12�֣�
�ɢ٢ڢ۽�ã�t=-
��t=-
��
��t=-
ʱ��m=
��-2���������⣬
���ϣ���ԲC���ڷ�������������Բ����R�������ǣ�-
��0��������13�֣�
| ||
| 2 |
| 3 |
������Բ���̿ɻ�Ϊ��
| x2 |
| 4b2 |
| y2 |
| b2 |
ֱ��l�ķ���Ϊy=x+
| 3 |
�ɷ�����
|
| 3 |
��5x2+8
| 3 |
��C��x1��y1����D��x2��y2������x1+x2=-
8
| ||
| 5 |
��
| AC |
| AD |
| BC |
| BD |
��4b•��-
8
| ||
| 5 |
32
| ||
| 5 |
����Բ������
| x2 |
| 4 |
��2������Բ�ĶԳ��ԣ�������P1��m��n����P2��m��-n����
��R��x���ϣ����R��t��0����
��ԲR�ķ���Ϊ����x-t��2+y2=��m-t��2+n2��
������Բ����֪������Բ�ϵĵ㵽��R�������Сֵ��|P1R|��
���M��x��y������ԲC������һ�㣬
��|MR|2=��x-t��2+y2=
| 3 |
| 4 |
��x=mʱ��|MR|2��С����m=-
| -2t | ||
|
| 4t |
| 3 |
��ԲR����F�����ԣ�-
| 3 |
��P1����Բ�ϣ���n2=1-
| m2 |
| 4 |
�ɢ٢ڢ۽�ã�t=-
| ||
| 2 |
| 3 |
��t=-
| 3 |
-4
| ||
| 3 |
���ϣ���ԲC���ڷ�������������Բ����R�������ǣ�-
| ||
| 2 |
���������⿼����Բ���̵���������Բ������Բ�Ƿ���ڵ��ж���������ʱҪ�������⣬ע�⺯���뷽��˼��ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
��ʵ��x��y����
����z=2x-y����Сֵ�ǣ�������
|
| A��1 | ||
| B��0 | ||
| C��-1 | ||
D��-
|
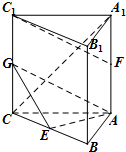 ��ͼ����������ABC-A1B1C1�У�AA1�͵���ABC��AB��AC��AC=AB=AA1��E��F�ֱ�����BC��A1A���е㣬GΪ��CC1�ϵ�һ�㣬��C1F��ƽ��AEG��
��ͼ����������ABC-A1B1C1�У�AA1�͵���ABC��AB��AC��AC=AB=AA1��E��F�ֱ�����BC��A1A���е㣬GΪ��CC1�ϵ�һ�㣬��C1F��ƽ��AEG��