题目内容
已知f(x)=x3+ax2+bx+c在x=1处的切线斜率为2,且导函数f′(x)的图象关于直线x=
对称.
(1)求a,b的值;
(2)若f(x)的图象与g(x)=x2的图象有且仅有三个公共点,求c的取值范围.
| 1 |
| 3 |
(1)求a,b的值;
(2)若f(x)的图象与g(x)=x2的图象有且仅有三个公共点,求c的取值范围.
考点:导数的运算,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:本题(1)利用导函数的运算和导数的几何意义可以得到相应参量的方程,解方程得本题结论;(2)本题通过导函数研究出函数图象的特征,根据图象的交点情况得到参数c满足的关系式,求出c的取值范围.
解答:
解:(1)f′(x)=3x2+2ax+b,
由已知得
_,
即
,
解得:
.
(2)由(1)知f(x)=x3-x2+x+
f(x)-g(x)=x3-2x2+x+c,
设F(x)=x3-2x2+x+
则F′(x)=3x2-4x+1=(3x-1)(x-1),
令F′(x)=0,得x=
或x=1,列表
两个图象有且仅有三个公共点,
只需
,
解得 -
<c<0.
∴c的取值范围是(-
,0).
由已知得
|
即
|
解得:
|
(2)由(1)知f(x)=x3-x2+x+
| c |
| , |
设F(x)=x3-2x2+x+
| c |
| , |
则F′(x)=3x2-4x+1=(3x-1)(x-1),
令F′(x)=0,得x=
| 1 |
| 3 |
| x | (-∞,
|
| (
| 1 | (1,+∞) | ||||||
| F′(x) | + | 0 | - | 0 | + | ||||||
| F(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
只需
|
解得 -
| 4 |
| 27 |
∴c的取值范围是(-
| 4 |
| 27 |
点评:本题考查的是函数的导数、导数的几何意义、利用导数研究函数的图象等知识,有一定的计算难度,本题属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=3sin(
已知函数f(x)=3sin(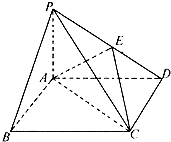 四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,E是侧棱PD的中点.
四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,E是侧棱PD的中点.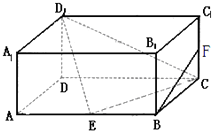 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.