题目内容
已知直线l1:(2a+b)x+(a+b)y+(a-b)=0与直线l2:m2x-
n2y+4=0.
(1)当实数a,b变化时,求证:直线l1过定点,并求出这个定点的坐标;
(2)若直线l2通过直线l1的定点,求点(m,n)所在曲线C的方程;
(3)在(2)的条件下,设F1(-1,0),F2(1,0),P(x0,0)(x0>0),过点P的直线交曲线C于A,B两点(A,B两点都在x轴上方),且
=3
,求此直线的方程.
| 4 |
| 3 |
(1)当实数a,b变化时,求证:直线l1过定点,并求出这个定点的坐标;
(2)若直线l2通过直线l1的定点,求点(m,n)所在曲线C的方程;
(3)在(2)的条件下,设F1(-1,0),F2(1,0),P(x0,0)(x0>0),过点P的直线交曲线C于A,B两点(A,B两点都在x轴上方),且
| F1A |
| F2B |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)l1的方程化为(2x+y+1)a+(x+y-1)b=0,令
,解得即可得出.
(2)由l2过定点(-2,3),代入l2化简得
+n2=1,即可得出.
(3)由
=3
,可得F1A∥F2B,且|F1A|=3|F2B|,可得|PF1|=3|PF2|,解出x0.设A(x1,y1),B(x2,y2).利用
=3
,及其
,解出即可.
|
(2)由l2过定点(-2,3),代入l2化简得
| m2 |
| 2 |
(3)由
| F1A |
| F2B |
| F1A |
| F2B |
|
解答:
(1)证明:l1的方程化为(2x+y+1)a+(x+y-1)b=0,
令
,解得
,
所以定点的坐标为(-2,3).
(2)解:由l2过定点(-2,3),代入得-2m2-4n2+4=0,化简得
+n2=1,
∴点(m,n)所在曲线C的方程为
+y2=1.
(3)解:∵
=3
,∴F1A∥F2B,且|F1A|=3|F2B|,
∴|PF1|=3|PF2|,
∴xx0+1=3(x0-1),解得x0=2.
∴P(2,0).
设A(x1,y1),B(x2,y2).
则
=(x1+1,y1),
=(x2-1,y2),
由
=3
,得
,
又由
,
联立解得
,
∴A(0,1),
∴PA的方程为x+2y-2=0.
令
|
|
所以定点的坐标为(-2,3).
(2)解:由l2过定点(-2,3),代入得-2m2-4n2+4=0,化简得
| m2 |
| 2 |
∴点(m,n)所在曲线C的方程为
| x2 |
| 2 |
(3)解:∵
| F1A |
| F2B |
∴|PF1|=3|PF2|,
∴xx0+1=3(x0-1),解得x0=2.
∴P(2,0).
设A(x1,y1),B(x2,y2).
则
| F1A |
| F2B |
由
| F1A |
| F2B |
|
又由
|
联立解得
|
∴A(0,1),
∴PA的方程为x+2y-2=0.
点评:本题考查了椭圆的标准方程及其性质、直线过定点问题、向量共线定理、平行线分线段成比例定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知f(
)=x-2
,则f(x)=( )
| x+2 |
| x+2 |
| A、f(x)=x2-2x-2(x≥-2) |
| B、f(x)=x2-2x-2(x≥0) |
| C、f(x)=x2-2x+2(x≥-2) |
| D、f(x)=x2-2x+2(x≥0) |
函数y=
的定义域为( )
| ||
| x |
| A、[-1,0) |
| B、(0,+∞) |
| C、[-1,0)∪(0,+∞) |
| D、(-∞,0)∪(0,+∞) |
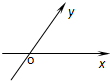 如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若
如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| A、x2+y2=2 |
| B、x2+y2=4 |
| C、x2+y2+xy=2 |
| D、x2+y2+xy=4 |