题目内容
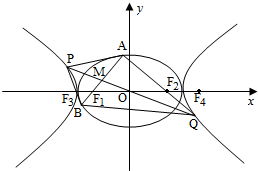 如图,O为坐标原点,椭圆C1:
如图,O为坐标原点,椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(Ⅰ)求C1、C2的方程;
(Ⅱ)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.
考点:圆锥曲线的综合,直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由斜率公式写出e1,e2,把双曲线的焦点用含有a,b的代数式表示,结合已知条件列关于a,b的方程组求解a,b的值,则圆锥曲线方程可求;
(Ⅱ)设出AB所在直线方程,和椭圆方程联立后得到关于y的一元二次方程,由根与系数的关系得到AB中点M的坐标,并由椭圆的焦点弦公式求出AB的长度,写出PQ的方程,和双曲线联立后解出P,Q的坐标,由点到直线的距离公式分别求出P,Q到AB的距离,然后代入代入三角形面积公式得四边形APBQ的面积,再由关于n的函数的单调性求得最值.
(Ⅱ)设出AB所在直线方程,和椭圆方程联立后得到关于y的一元二次方程,由根与系数的关系得到AB中点M的坐标,并由椭圆的焦点弦公式求出AB的长度,写出PQ的方程,和双曲线联立后解出P,Q的坐标,由点到直线的距离公式分别求出P,Q到AB的距离,然后代入代入三角形面积公式得四边形APBQ的面积,再由关于n的函数的单调性求得最值.
解答:
解:(Ⅰ)由题意可知,e1=
,e2=
,且|F1F2|=2
.
∵e1e2=
,且|F2F4|=
-1.
∴
•
=
,且
-
=
-1.
解得:a=
,b=1.
∴椭圆C1的方程为
+y2=1,双曲线C2的方程为
-y2=1;
(Ⅱ)由(Ⅰ)可得F1(-1,0).
∵直线AB不垂直于y轴,
∴设AB的方程为x=ny-1,
联立
,得(n2+2)y2-2ny-1=0.
设A(x1,y1),B(x2,y2),M(x0,y0),
则y1+y2=
,y0=
,y1y2=-
.
则|AB|=
=
=
.
∵M在直线AB上,
∴x0=
-1=-
.
直线PQ的方程为y=
x=-
x,
联立
,得x2-2×(-
x)2-2=0.
解得x2=
,代入y=-
x 得y2=
.
由2-n2>0,得-
<n<
.
∴P,Q的坐标分别为(-
,
),(
,-
),
则P,Q到AB的距离分别为:d1=
,d2=
.
∵P,Q在直线A,B的两端,
∴d1+d2=
.
则四边形APBQ的面积S=
|AB|(d1+d2)=2
•
.
∴当n2=0,即n=0时,四边形APBQ面积取得最小值2.
1-
|
1+
|
| a2-b2 |
∵e1e2=
| ||
| 2 |
| 3 |
∴
1-
|
1+
|
| ||
| 2 |
| a2+b2 |
| a2-b2 |
| 3 |
解得:a=
| 2 |
∴椭圆C1的方程为
| x2 |
| 2 |
| x2 |
| 2 |
(Ⅱ)由(Ⅰ)可得F1(-1,0).
∵直线AB不垂直于y轴,
∴设AB的方程为x=ny-1,
联立
|
设A(x1,y1),B(x2,y2),M(x0,y0),
则y1+y2=
| 2n |
| n2+2 |
| n |
| n2+2 |
| 1 |
| n2+2 |
则|AB|=
| 1+n2 |
| (y1+y2)2-4y1y2 |
=
| 1+n2 |
(
|
2
| ||
| n2+2 |
∵M在直线AB上,
∴x0=
| n2 |
| n2+2 |
| 2 |
| n2+2 |
直线PQ的方程为y=
| y0 |
| x0 |
| n |
| 2 |
联立
|
| n |
| 2 |
解得x2=
| 4 |
| 2-n2 |
| n |
| 2 |
| n2 |
| 2-n2 |
由2-n2>0,得-
| 2 |
| 2 |
∴P,Q的坐标分别为(-
|
|
|
|
则P,Q到AB的距离分别为:d1=
|n•
| ||||||||
|
|-n•
| ||||||||
|
∵P,Q在直线A,B的两端,
∴d1+d2=
|2n•
| ||||||||
|
则四边形APBQ的面积S=
| 1 |
| 2 |
| 2 |
|
∴当n2=0,即n=0时,四边形APBQ面积取得最小值2.
点评:本题考查圆锥曲线方程的求法,是直线与圆锥曲线、圆锥曲线与圆锥曲线间的关系的综合题,考查了椭圆与双曲线的基本性质,关键是学生要有较强的运算能力,是压轴题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
| A、60种 | B、70种 |
| C、75种 | D、150种 |

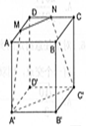 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题: