题目内容
一个盒子里装有三张卡片,分别标记有1,2,3,这三张卡片除标记的数字外完全相同,随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(Ⅰ)求“抽取的卡片上的数字满足a+b=c”的概率;
(Ⅱ)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
(Ⅰ)求“抽取的卡片上的数字满足a+b=c”的概率;
(Ⅱ)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)所有的可能结果(a,b,c)共有3×3×3=27种,而满足a+b=c的(a,b,c有计3个,由此求得“抽取的卡片上的数字满足a+b=c”的概率.
(Ⅱ)所有的可能结果(a,b,c)共有3×3×3种,用列举法求得满足“抽取的卡片上的数字a,b,c完全相同”的(a,b,c)共计三个,由此求得“抽取的卡片上的数字a,b,c完全相同”的概率,再用1减去此概率,即得所求.
(Ⅱ)所有的可能结果(a,b,c)共有3×3×3种,用列举法求得满足“抽取的卡片上的数字a,b,c完全相同”的(a,b,c)共计三个,由此求得“抽取的卡片上的数字a,b,c完全相同”的概率,再用1减去此概率,即得所求.
解答:
解:(Ⅰ)所有的可能结果(a,b,c)共有3×3×3=27种,
而满足a+b=c的(a,b,c)有(1,1,2)、(1,2,3)、(2,1,3),共计3个,
故“抽取的卡片上的数字满足a+b=c”的概率为
=
.
(Ⅱ)满足“抽取的卡片上的数字a,b,c完全相同”的(a,b,c)有:
(1,1,1)、(2,2,2)、(3,3,3),共计三个,
故“抽取的卡片上的数字a,b,c完全相同”的概率为
=
,
∴“抽取的卡片上的数字a,b,c不完全相同”的概率为1-
=
.
而满足a+b=c的(a,b,c)有(1,1,2)、(1,2,3)、(2,1,3),共计3个,
故“抽取的卡片上的数字满足a+b=c”的概率为
| 3 |
| 27 |
| 1 |
| 9 |
(Ⅱ)满足“抽取的卡片上的数字a,b,c完全相同”的(a,b,c)有:
(1,1,1)、(2,2,2)、(3,3,3),共计三个,
故“抽取的卡片上的数字a,b,c完全相同”的概率为
| 3 |
| 27 |
| 1 |
| 9 |
∴“抽取的卡片上的数字a,b,c不完全相同”的概率为1-
| 1 |
| 9 |
| 8 |
| 9 |
点评:本题主要考查相互独立事件的概率乘法公式的应用,属于中档题.

练习册系列答案
相关题目
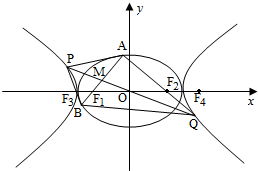 如图,O为坐标原点,椭圆C1:
如图,O为坐标原点,椭圆C1: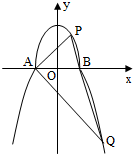 如图,曲线C由上半椭圆C1:
如图,曲线C由上半椭圆C1: