题目内容
设函数f(x)=ax+1在(-1,1)上有零点,则a的取值范围是 .
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:函数f(x)=ax+1在(-1,1)上单调且f(x)=ax+1在(-1,1)上有零点,则f(-1)f(1)<0,从而解出.
解答:
解:∵函数f(x)=ax+1在(-1,1)上单调,
又∵f(x)=ax+1在(-1,1)上有零点,
∴f(-1)f(1)<0,
即(1-a)(1+a)<0,
则a>1或a<-1,
故答案为:a>1或a<-1.
又∵f(x)=ax+1在(-1,1)上有零点,
∴f(-1)f(1)<0,
即(1-a)(1+a)<0,
则a>1或a<-1,
故答案为:a>1或a<-1.
点评:本题考查了函数的零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
设f(x)=
x3+ax2+5x+6在区间[1,3]上为单调递减函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、(-∞,-
| ||||
| B、(-∞,-3] | ||||
C、(-∞,-3]∪[-
| ||||
D、(-
|
一物体的运动方程为S=6t2+3t-2,则它在t=3时的瞬时速度为( )
| A、36 | B、39 | C、12 | D、33 |
下列函数中是偶函数的是( )
| A、y=x-2 | ||
| B、y=x2,x∈(-2,3] | ||
C、y=-
| ||
| D、y=x3 |
已知函数f(x)=x2,则下列各式中正确的是( )
| A、f(-1)>f(2)>f(-3) |
| B、f(2)>f(-1)>f(-3) |
| C、f(-3)>f(2)>f(-1) |
| D、f(-3)>f(-1)>f(2) |
“m<
”是“方程x2+x+m=0有实数解”的( )
| 1 |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
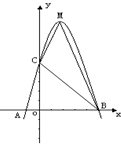 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.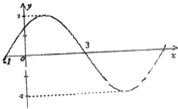 已知f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
已知f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<